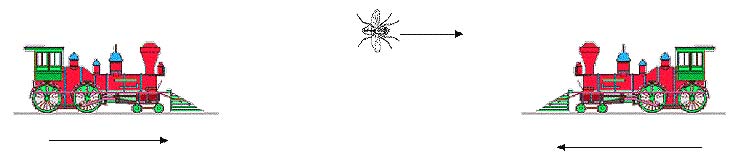
Two trains are approaching each another and a fly is buzzing back and forth between the two trains. Given the (constant) speed of the trains and their initial separation distance, and the (constant) speed of the fly, calculate how far the fly will travel before the trains collide.

 

This problem appears to have been first posed by Charles Ange Laisant (1840–1921) in his Initiation Mathématique. There is a long-winded method of getting the answer and a much shorter way.

 

Suppose the trains start out 200 miles apart and are each traveling at 50 mph, and the fly – a speedster of its kind – is moving at 75 mph. The long method involves considering the length of the back-and-forth path that the fly takes and evaluating this as the sum of an infinite series. The quick solution is to notice that the trains will collide in 2 hours and that in this time the fly will travel 2 × 75 = 150 miles!

 

When this problem was put to John von Neumann, he immediately gave the correct answer. The poser, assuming he had spotted the shortcut, said: "It is very strange, but nearly everyone tries to sum the infinite series." Von Neumann replied: "What do you mean, strange? That's how I did it!"