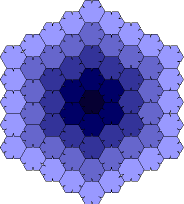
The Heesch number is the maximum number of times that a closed plane figure can be completely surrounded by copies of itself. The Heesch number of a triangle, quadrilateral, regular hexagon, or any other single shape that can completely tile the plane (see tiling), is infinity. Heesch's problem is to find the largest possible finite Heesch number, or, more generally, what values other than zero and infinity can occur as Heesch numbers. In considering this problem, it's helpful to define the Heesch number more precisely. In a tiling, the first corona of a tile is the set of all tiles that have a common boundary point with the tile, including the original tile itself. The second corona is the set of tiles that share a point with anything in the first corona; and so on. The Heesch number of a shape is the maximum value of k for which all tiles in the k-th corona of any tiling are congruent to that shape. For a long time the record holder for the largest finite value of k was a shape found by the American computer scientist Robert Ammann, which consisted of a regular hexagon with small projections on two sides and matching indentations on three sides. This was thought to have a Heesch number of three; however, in 2000, Alex Day argued that the Ammann hexagon actually has a Heesch number of four, though there is a dispute about whether the difference has to do with a definition of tiling. In any event, it has since been shown by Casey Mann, of the University of Arkansas that there exists an infinite family of tiles (consisting of indented and outdented pentahex) with Heesch number five (or six by Day's reckoning) – the largest finite value currently known.

 

It remains an open issue whether any polygon has higher Heesch number, but these new techniques seem very powerful and likely to lead to further results. Mann believes that more rounded polyominos than the long skinny ones he's been using may have a better chance of giving unbounded Heesch numbers.

 

The Heesch number question seems closely connected to two other famous open tiling problems: does there exist an algorithm for determining whether a shape can tile, and does there exist a shape that can only tile aperiodically? Aperiodic tiling seems to act as a barrier to the existence of tiling algorithms, so it isn't expected that both of these problems have the same answer. On the other hand, if no finite Heesch number is larger than some k, then it seems that this could be used as the basis of an algorithm to test whether a shape tiles: simply attempt to fill out a tiling to the (k + 1)st corona; if successful, the shape must tile the plane, and if not, the shape does not tile. Similar questions can also be asked about Heesch numbers for tilings in higher dimensions.