Kakeya needle problem

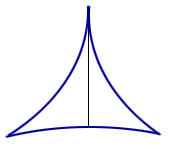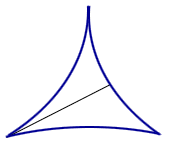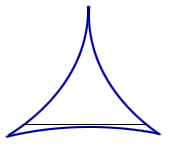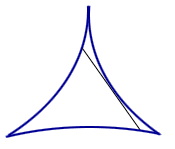
Line segment rotating in a 3-cusped hypocycloid

A famous problem named after the Japanese mathematician Soichi Kakeya, who first posed it in 1917. It asks: what is the smallest-area plane figure inside which a unit straight line segment can be rotated through 180°?

For some years, the answer was thought to be a deltoid. However, in 1928, the Russian mathematician Abram Besicovitch shocked the mathematical world by showing that the problem had no answer or, to be more precise, that there was no minimum area.¹ In 1917 Besicovitch had been working on a problem in Riemann integration, and had reduced it to the question of existence of planar sets of measure 0, which contain a line segment in each direction. He then constructed such a set, and published his construction in a Russian journal in 1920. Due to the civil war and the blockade, there was hardly any communication between Russia and the rest of the world at the time, so that Besicovitch hadn't heard about the challenge posed by Kakeya. Several years later, after he had left Russia and learned about the needle problem, Besicovitch modified his original construction and was able to give the starling answer that the area in question may be made arbitrarily small.

Reference

Besicovitch, A. S. "On Kakeya's Problem and a Similar One." Math. Z., 27: 312-320, (1928).

Related category

• GEOMETRY

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP