A deltoid is a hypocycloid with three cusps, also known as a tricuspoid or Steiner's hypocycloid after the Swiss mathematician Jakob Steiner who investigated the curve in 1856.

 

The deltoid, so-named because it looks like an uppercase Greek delta (Δ), is formed by a point on the circumference of a circle rolling inside another circle with a radius three times as large. Among the first to study its properties was Leonhard Euler while working on a problem in optics in 1745.

 

The parametric equations of the cycloid with inner circle of radius r are:

 

    x(t ) = 2r cos t + r cos 2t
    y(t ) = 2r sin t - r sin 2t

 

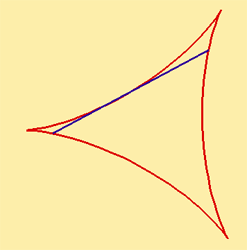
The length of the path of the deltoid is 16r/3, and the area inside the deltoid is 2πr ². If a tangent is drawn to the deltoid at some point, P, and the points where the tangent crosses the deltoids other two branches are called points A and B, then the length of AB equals 4r. If the deltoid's tangents are drawn at points A and B, they will be perpendicular, and they will intersect at a point inside the deltoid that is the 180° rotation of point P about the center of the fixed circle.