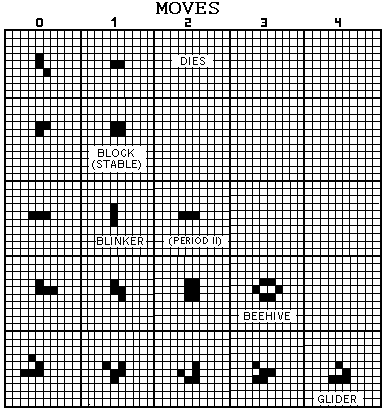
Conway's Game of Life is the best known example of a cellular automaton; it was invented by John Conway and first brought to public attention in Martin Gardner's Scientific American column in October 1970. Conway's goal in creating Life was to devise a universal Turing machine – a sort of infinitely programmable computer. John von Neumann had described such a system in the 1950s, but it had very complex rules; Conway wanted to find one that was much simpler to describe and to operate.

 

Life is played on a grid of squares on which each cell is either alive (occupied) or dead (empty). The game starts from an arbitrary initial configuration of live cells, and then progresses through generations as the life and death rules are applied. These rules are very simple: (1) A live cell survives to the next generation if it has two or three neighbors. (2) A live cell dies if it has four or more neighbors (overcrowding) or if it has only one neighbor or none (isolation). (3) A dead cell becomes a live cell in the next generation if it has exactly three neighbors (birth).

 

The rules of Life were developed over a two-year-period during tea and coffee breaks by Conway and a group of graduate students and colleagues. Because Go boards and counters were used at this stage, instead of computers, it was important to have a death rule so that populations didn't tend to explode and quickly race off the board. On the other hand, to enable sufficiently interesting behavior that the game had a chance of being a universal system, it was equally important to have a birth rule that prevented populations from dying out. The rules eventually chosen provided a balance between birth and death so that the system tended to be fairly stable yet interesting enough to study. An early sign of success was the discovery of patterns, known as 'gliders,' that kept their shape while drifting across the plane. This was a hopeful step toward proving universality because it showed that the system had a way to transmit information from one place to another. Conway and his group went on to build nearly all the necessary configurations for arbitrary computations: AND gates, OR gates, and so on, just like the components of an ordinary computer. What they needed next was a way of producing gliders at will – a 'glider gun.' At this point, Conway sent a letter describing Life and the early finding's to Martin Gardner, offering a prize of $50 for a configuration whose population tended towards infinity. The resulting Scientific American column sparked the public's imagination and very quickly a glider gun was discovered by a group at the Massachusetts Institute of Technology led by R. W. Gosper. Within two weeks of the discovery of the glider gun, both Conway's group and the group at MIT had shown that the system was indeed universal.