standard deviation
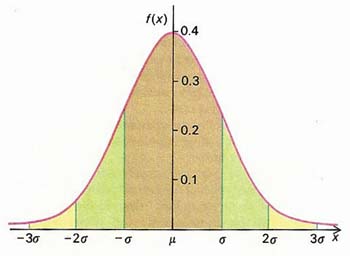
Over 68% of a population exhibiting a normal distribution for some property lie within one standard deviation (σ) of the mean (μ). Over 95% lie within μ±2σ and over 99% within μ±3σ. The total population in this example is unity (1).
Standard deviation is a measure of the spread of a set of data. For a normal distribution, the standard deviation gives a measure of the width of the tails of the distribution function.
The sample standard deviation is the positive square root of the sample variance s2, where variance is defined as the arithmetic mean of the squares of the deviations of the members of a sample from the arithmetic mean of the sample. The population standard deviation σ is given by the square root of the population variance:
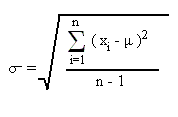
where n is the number of observations, μ is the mean, and xi the ith value.
In a normal or Gaussian distribution, about 68.3% of the population lies within one standard deviation of the mean.


