tensor
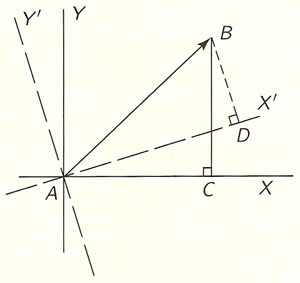
Figure 1.
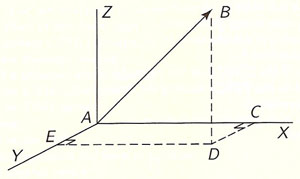
Figure 2.
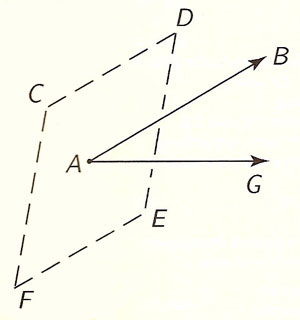
Figure 3.
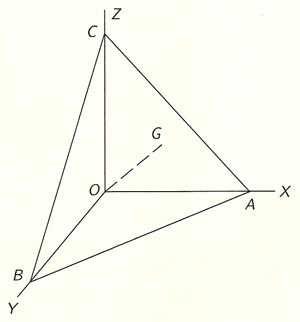
Figure 4.
A tensor is a generalization of a vector. Tensors originated in the 19th century as an abstract mathematical concept. A tensor is specified in terms of a set of coordinates, so that its form changes if a different set of mathematical coordinates is chosen. However, tensors have the property that any equation involving them that is true in one set of coordinates remains true when the equation is written in the same form in any other set of coordinates. A tensor can be thought of as providing information about the rate at which things are changing at a point.
An ordinary vector can be described as a tensor of the first rank and a 2-dimensional matrix as a tensor of the second rank.
Gentle introduction to tensors
by Lillian R. Lieber from her book The Einstein Theory
of Relativity [reproduced with permission; original, easy-to-read layout
retained]
The reader is no doubt familiar
with the words "scalar" and "vector."
A scalar is a quantity which
has magnitude only,
whereas
a vector has
both magnitude and direction.
Thus,
if we say that
the temperature at a certain place
is 70° Fahrenheit,
there is obviously NO DIRECTION
to this temperature,
and hence
TEMPERATURE is a SCALAR.
But
if we say that
an airplane has gone
one hundred miles east,
obviously its displacement
from its original position
is a VECTOR,
whose MAGNITUDE is 100 miles,
and whose DIRECTION is EAST.
Similarly,
a person's AGE is a SCALAR,
whereas
the VELOCITY with which an object moves
is a VECTOR,
and so on;
the reader can easily
find further examples
of both scalars and vectors.
We shall now discuss
some quantities
which come up in our experience
and which are
neither scalars nor vectors,
but which are called
TENSORS.
And,
when we have illustrated and defined these,
we shall find that
a SCALAR is a TENSOR whose RANK is ZERO,
and
a VECTOR is a TENSOR whose RANK is ONE,
and we shall see what is meant by
a TENSOR of RANK TWO, or THREE, etc.
Thus "TENSOR" is a more inclusive term
of which "SCALAR" and "VECTOR" are
SPECIAL CASES.
Before we discuss
the physical meaning of
a tensor of rank two,
let us consider
the following facts about vectors.
Suppose that we have
any vector, AB, in a plane,
and suppose that
we draw a pair of rectangular axes,
X and Y (Figure 1).
Drop a perpendicular BC
from B to the X-axis.
Then we may say that
AC is the X-component of AB;
for,
as we know from
the elementary law of "The parallelogram
of forces,"
if a force AC acts on a particle
and CB also acts on it,
the resultant effect is the same
as the of a force AB alone.
And that is why
AC and CB are called
the "components" of AB.
Of course if we had used
the dotted lines as axes instead,
the components of AB would now be AD and DB.
In other words,
the vector AB may be broken up
into components
in various ways,
depending on our choice of axes.
Similarly,
if we use THREE axes in SPACE
rather than two in a plane,
we can break up a vector
into THREE components
as shown in Figure 2.
By dropping the perpendicular BD
from B to the XY-plane,
and then drawing
the perpendiculars DC and DE
to the X and Y axes, respectively,
we have the three components of AB,
namely,
AC, AE, and DB,
and, as before,
the components depend upon
the particular choice of axes.
Let us now illustrate
the physical meaning
of a tensor of rank two.
Suppose we have a rod
at every point of which
there is a certain strain
due to some force acting on it.
As a rule the strain
is not the same at all points,
and, even at any given point,
the train is not the same in
all directions.
Now, if the STRESS at the point A
(that is, the FORCE causing the strain at A)
is represented
both in magnitude and direction
by AB (Figure 3)
and if we are interested to know
the effect of this force upon
the surface CDEF (through A),
we are obviously dealing
with a situation which depends
not on a SINGLE vector
but on TWO vectors.
Namely,
one vector, AB,
which represents the force in question,
and another vector
(call it AG),
whose direction will indicate
the ORIENTATION of this surface CDEF,
and whose magnitude will represent
the AREA of CDEF.
In other words,
the effect of a force upon a surface
depends NOT ONLY on the force itself
but ALSO on the
size and orientation of the surface.
Now, how can we indicate
the orientation of a surface
by a line?
If we draw a line through A
in the plane CDEF,
obviously we can draw this line
in many different directions,
and there is no way
of choosing any one of these
to represent the orientation of this surface.
BUT,
if we take a line through A
PERPENDICULAR to the plane CDEF,
such a line is UNIQUE
and CAN therefore be used
to specify the orientation
of the surface CDEF.
Hence, if we draw a vector, AG,
in a direction perpendicular to CDEF
and of such a length that
it represents the magnitude of
the area of CDEF,
then obviously
this vector AG
indicates clearly
both the SIZE and ORIENTATION
of the surface CDEF.
Thus,
the STRESS at A
upon the surface CDEF
depends upon the TWO vectors,
AB and AG,
and is called a TENSOR of RANK TWO.
Let us now find a convenient way
of representing this tensor.
And, in order to do so,
let us consider the stress, F,
upon a small surface, dS,
represented in the figure below
by ABC (= dS).
Now if OG, perpendicular to ABC,
is the vector which represents
the size and orientation of ABC (Fig 4),
then,
it is quite easy to see
that the X-component of OG
represents in magnitude and direction
the projection OBC of ABC upon the YZ-plane.
And similarly,
the Y and Z components of OG
represent the projections
OAC and OAB, respectively.
Now, if the force F,
which is itself a vector,
acts on ABC,
we can examine its total effect
by considering separately
the effects of its three components
fX, fY, and fZupon EACH of the three projections
OBC, OAC, and OAB.Let us designate these projections
by dSX, dSY, and dSZ, respectively.
Now,
since fX
(which is the X-component of F)
acts upon EACH one of the three
above-mentioned projections,
let us designate the pressure
due to this component alone
upon the three projections
pXX, pXY, pXZ,
respectively.
We must emphasize
the significance of this notation:
In the first place,
the reader must distinguish between
the "pressure" on a surface
and the "force" acting on the surface.
The "pressure" is
the FORCE PER UNIT AREA.
So that
the TOTAL FORCE is obtained by
MULTIPLYING
the PRESSURE by the AREA of the surface.
Thus the product
pXX.dSX
gives the force acting upon
the projection dSX
due to the action of fX ALONE.
Note the DOUBLE subscripts in
pXX, pXY, pXZ:
The first one obviously refers to the fact
that
these three pressures all emanate
from the component fX alone;
whereas,
the second subscript designates
the particular projection upon which
the pressure acts.
Thus pXY means
the pressure due to fX
upon the projection dSY,
etc.
It follows therefore that
fX = pXX.dSX + pXY.dSY + pXZ.dSZ
And, similarly,
fY = pYX.dSX + pYY.dSY + pYZ.dSZ
and
fZ = pZX.dSX + pZY.dSY + pZZ.dSZ
Hence the TOTAL STRESS, F,
on the surface dS,
is
F = fX + fY + fZ
F = fX = pXX.dSX + pXY.dSY + pXZ.dSZ
+ fY = pYX.dSX + pYY.dSY + pYZ.dSZ
+ fZ = pZX.dSX + pZY.dSY + pZZ.dSZ
Thus we see that
stress is not just a vector,
with three components in
three-dimensional space
but has NINE components
in THREE-dimensional space.
Such a quantity is called
a TENSOR OF RANK TWO.
It is obvious that
if we were dealing with a plane
instead of with
three-dimensional space,
a tensor of rank two would then have
only FOUR components instead of nine,
since each of the two vectors involved
has only two components in a plane,
and therefore,
there would now be only
2 × 2 components for the tensor
instead of 3 × 3 as above.
And, in general,
if we are dealing with
n-dimensional space,
a tensor of rank two
has n2 components
which are therefore conveniently written
in a SQUARE array
as was done above.
Whereas,
in n-dimensional space,
a VECTOR has only n components.
Thus,
a VECTOR in a PLANE
has TWO components;
in THREE-dimensional space it has
THREE components,
and so on.
Hence,
the components of a VECTOR
are therefore written
in a SINGLE ROW;
instead of in a SQUARE ARRAY
as in the case of a TENSOR of RANK TWO.
Similarly,
in n-dimensional space
a TENSOR of rank THREE has n3 components,
and so on.
To sum up:
In n-dimensional space,
a VECTOR has n components,
a TENSOR of rank TWO has n2 components,
a TENSOR of rank THREE has n3 components,
and so on.


