absolute zero

The unattainability of absolute zero is graphically demonstrated by this illustration, in which the absolute temperature is plotted in degrees kelvin on a logarithmic scale rather than a normal linear scale. The logarithmic scale better represents the task confronted by low-temperature physicists, since in nature the ratio of two absolute temperature T1/T2, is more important than their difference T1 – T2. Thus the distance from 10 K to 1 K is just as great as the distance from 0.001 K to 0.0001 K. On the logarithmic scale, the point at which T = 0K is infinitely far to the left.

McGill University student Cory Dean works on a dilution refrigerator capable of reaching 8 mK above absolute zero.
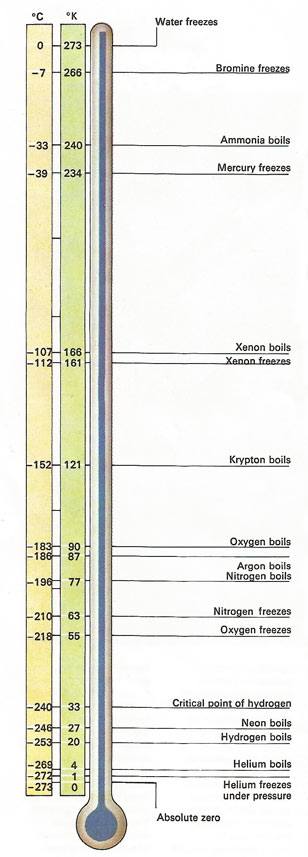
The temperature on this diagram are stated in both the Kelvin (absolute) and Celsius (centigrade) scales, below a temperature equivalent to the melting-point of ice in equilibrium with water.

Liquid air has a temperature of only 83 K (–190 °C) and thus a flower dipped in it will solidify completely as all the fluid in its cells freezes. When this happens the flower becomes so brittle that it can be broken into small pieces with a blow from a hammer. Liquid air is used industrially for freezing other substances and for the commercial production of oxygen and nitrogen.
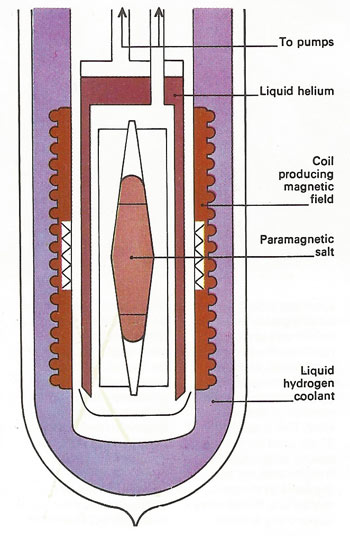
To approach absolute zero – below 1 K (–272 °C) – a phenomenon called adiabatic demagnetization of paramagnetic salt is one that acts as a magnet only in a strong magnetic field. The field forces the molecules into an orderly array. If there is no exchange of heat energy during this process than it is said to be adiabatic. But when they are ordered the molecules have less energy and the balance is given up to the salt, raising its temperature above 1 K. Liquid helium is then used to re-cool the salt. If it is now demagnetized, its molecules become disordered. The energy for this can come only from the salt and its temperature falls below 1 K.
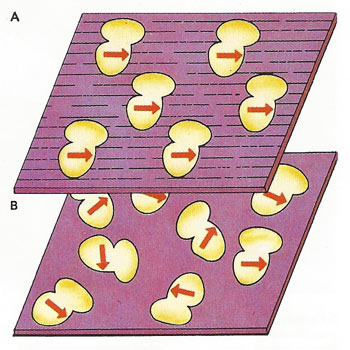
The molecules of a paramagnetic salt are normally in continual disordered motion, even if the temperature is as low as 1 K (–272 °C). As long as the molecules behave in this way there is no part of the salt that appears to be like either pole of a magnet. As soon as the salt is placed in a magnetic field [A], however, the molecular magnets line up along the field and endow the bulk substance with north and south magnetic poles. Molecular disorder returns when the field is removed [B].
Absolute zero, in theory, is the lowest possible temperature, and therefore the lowest possible total energy of a system. Although it might be expected that all particle motion would stop at absolute zero, this is not in fact the case. The Heisenberg uncertainty principle asserts that even at the minimum conceivable temperature, subatomic particles would still possess a residual kinetic energy known as zero point energy. A strange outcome of this fact is that the closely packed electrons in a metal at absolute zero would have the same energy as an ordinary gas at 50,000°C. Thus, although at absolute zero a system's entropy is zero, the total energy of a system is not zero.
Temperatures within a few billionths of a degree of absolute zero have been achieved in the laboratory. At such low temperatures, substances have been seen to enter a peculiar state, known as the Bose-Einstein condensate, in which their quantum wave functions merge and particles lose their individual identities.
Denoted by zero degrees on the kelvin temperature scale (0K = –273.16°C = –459.6 °F), absolute zero is physically unattainable according to the third law of thermodynamics. At first sight, this might seem unreasonable. There is no upper temperature limit, so why should there be a lower one? In trying to understand this, it is helpful to think in terms of temperature ratios rather than temperature differences – the ratio from 10,000 K to 1,000 K, say, being the same as that from 0.001 K to 0.0001 K. Just as by supplying more and more energy to a system we can add as many zeros before the decimal point of the kelvin reading as we choose, so by continuing to take energy out of a system we can add an arbitrary number of zeros after the decimal point. Yet just as we can never reach an infinitely high temperature, so we can never attain an infinitely low one – absolute zero itself.
In a deep sense, absolute zero lies at the asymptotic limit of low energy just as the speed of light lies, for particles with mass, at the asymptotic limit of high energy. In both cases, energy of motion – kinetic energy – is the key quantity involved. At the high energy end, as the average speed of the particles of a substance approaches the speed of light, the temperature rises without limit.
Towards absolute zero
Every substance contains a certain amount of heat, even a relatively cold substance such as ice. The heat is the result of the continual motion of the substance's molecules which, by that motion, possess kinetic energy. Temperature is a measure of the average kinetic energy of the molecules. The cooler the substance becomes the less its molecules move. Thus it should be possible to continue cooling to the point at which molecular movement ceases completely. This point, "absolute zero", is of great interest to scientists but in practice is unattainable. At temperatures close to absolute zero some materials exhibit remarkable properties, such as superconductivity and superfluidity.
Calculation of absolute zero
On the centigrade temperature scale, absolute zero is 273.16 degrees below the freezing point of water. Its value can be predicted as a result of the behavior of gases when they are heated or cooled, When heated, a "perfect" gas expands in volume (V) proportionally to its absolute temperature (T) if its pressure (P) is kept constant. Its pressure increases in the same proportion if its volume is kept constant. The reverse occurs on cooling, according to the equation PV = RT where R is known as the universal gas constant. The pressure actually falls by a factor of 1/273.16 for every 1°C temperature decrease. Thus at -273.16 °C zero pressure would be reached and this must be the absolute zero of temperature.
Absolute zero is usually denoted as 0 on the Kelvin scale of temperature, named after the British scientist William Thomson, Baron Kelvin of Largs. Its temperature increments equal those on the centigrade or Celsius scale. Thus 0K is the same as –273°C (absolute zero temperature is usually rounded to –273°C, or –460 on the Fahrenheit scale) and 273 K equals 0°C – the freezing point of water.
Aiming at absolute zero
Gas temperatures can be lowered by first compressing the gas in a fixed-volume enclosure and then removing the resultant heat with, for example, a surrounding water jacket. If the gas is then allowed to escape into a larger volume it becomes even cooler because its molecules lose kinetic energy during the expansion. This cycle is used in a refrigerator and can liquefy and even freeze many gases.
The gas most useful in experiments at very low temperatures had been helium, the gas with the lowest boiling-point, 4.2 K (–269°C). The temperature of liquid helium can be further reduced to 1 K by vacuum pumping the gas above the level of the liquid to reduce its pressure and thereby force down the boiling-point. Liquid helium is generally produced in an air liquefaction plant as one of the rare gases left after oxygen and nitrogen have been liquefied.
Below 1 K it is difficult to achieve further cooling and a low-temperature effect that occurs in some solids is used. Some salts act as magnets when immersed in a strong magnetic field but stop being magnetic when the field is removed, a phenomenon known as paramagnetism. When the salt is magnetized its molecules line up in the field but are disarranged when the field is removed. If a paramagnetic solid is cooled to 1 K by liquid helium that is allowed to evaporate, heat energy is removed from the solid. When a strong magnetic field is switched on, the molecules align themselves and create heat by their motion. This is removed by the surrounding helium gas, which is pumped away. When the field is switched off, the molecules become disordered and cause a further lowering of the solid's internal energy. The cold salt can then absorb heat from a second helium container. A cycle of magnetization and demagnetization can produce temperatures of a few thousandths of a degree kelvin.
Superfluidity and superconductivity
Liquid helium at very low temperatures is not only difficult to produce but behaves in a most unusual way. Fast boiling occurs as the vapor pressure falls but at 2.18 K the internal bubbling of helium gas suddenly ceases, although boiling continues. Below this so-called "lambda point" liquid helium exhibits "superfluidic" properties.
Near absolute zero, certain substances show remarkable properties; for example, a kind of perpetual motion in electric current becomes possible – that is, some metals and alloys exhibit superconductivity. As their temperature is lowered (for example, to 7 K for lead) the electrical resistance of the material disappears completely. If an electric current can be made to flow in a ring of such metal it continues to flow. Current has been kept flowing unattenuated in this way for up to several years.
Superconductivity was discovered by the Dutch physicist Heike Kamerlingh Onnes. It can theoretically be used as the basis for some computer memories, for once stored in a superconductor, information remains unaltered. A magnetic field of sufficient strength can destroy the superconducting state and this effect can be used to achieve a high-speed current-switching facility. As a superconducting material has zero electrical resistance, very high currents can pass through it. As a result, superconducting windings for electromagnets can be used to generate extremely powerful magnetic fields.

