speed of light


Figure 1. The blue glow coming from the water surrounding this nuclear reactor is known as Cerenkov radiation. It is produced because nuclear particles emitted by the reactor are moving faster than light does itself in water, which slows light by about a quarter. The particles cause a shock wave to be produced in the water, just as a supersonic plane produces a shock wave in air. We hear the sound shock wave as a supersonic boom and see the light shock wave as blue light. The production of Cerenkov radiation is used as a method of detecting fast-moving particles in nuclear physics. The radiation was first observed by the Russian physicist Paul Cerenkov (sometimes known as Cherenkov) in 1934.
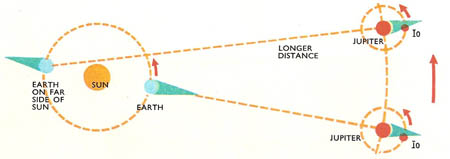
Figure 2. Römer's method for finding the speed of light. When Jupiter is a long way from Earth, its satellite Io eclipses later than would be expected. This is because the light takes more time to travel the extra distance.
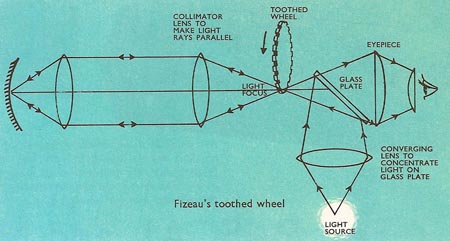
Figure 3. Another determination was made by Armand Fizeau (1819–1896) in 1849. Light was reflected through the teeth of a rotating wheel to a mirror and back through the teeth to the observer. The light was seen only when the wheel spun so fast that no teeth blocked its return journey. From the spacing of the teeth, the speed of the rotation of the wheel and the distance of the mirror (98 km), the velocity of light could be accurately calculated.

Figure 4. Foucault's method for measuring the speed of light.
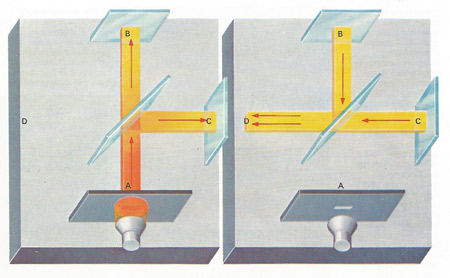
Figure 5. The Michelson-Morley experiment, first made in 1881, used an interferometer to produce a pattern of interference fringes from two beams at right-angles. The Earth's motion was expected to make the light move faster along.
Designated by the letter "c," the speed of light in empty space is 299,793 kilometers per second (186,282 miles per second) so that light takes only 1.3 seconds to travel from the Moon to Earth. The speed of light has the same value independent of the relative velocity between source and observer, an experimental fact that makes sense only if relative motion changes the relationship between space and time intervals to keep the distance covered by light per unit time the same for all observers. The fact that space and time are interchangeable to keep the speed of light constant implies that, in some sense, space and time must be the same, despite our habit of measuring space in meters and time in seconds. But if time and space are similar to the extent that they can be converted one into the other, then a quantity is needed to convert the units – something measured in meters per second that can be used to multiply seconds of time to get meters of space. This universal conversion factor is the speed of light. The reason it is limited arises simply from the fact that a finite amount of space is equivalent to a finite amount of time.
The "speed of light" can also mean the speed at which light travels in a given medium. For example, light travels only two-thirds as quickly in glass as it does in a vacuum. The change in velocity when light enters a medium such as air, water or glass causes the light to bend on entering a different medium and refraction occurs. The refractive index of a medium is the ratio of the velocity of light in a vacuum to its velocity in the medium. For example, the refractive index of water is 1.333 or 4/3, and thus the velocity of light in water is only three-quarters of its velocity in a vacuum.
If something, such as a subatomic particle, travels faster through a medium than light does, the result is a kind of electromagnetic shock wave known as Cerenkov radiation (Figure 1). However, there is no violation of the laws of physics, since the universal speed limit is how fast light travels in a vacuum.
The speed of light also limits the maximum rate at which information can be transferred from one place to another. Although nonlocal effects in quantum mechanics, such as teleportation, may be instantaneous even over great distances, they do not violate the special theory of relativity because no matter, energy, or information is moved faster than light. However, various ways by which the "light barrier" might be broken or circumvented have been proposed by theoretical physicists.
Any particles of zero rest mass, such as photons, travel at the speed of light. Massive particles approach the speed of light when their energy is very large relative to their rest energy.
Measuring the speed of light
Because of the enormous distance traveled by light in a second it isn't surprising that the first attempts to measure the speed of light failed. These were performed by Galileo who tried to find the time taken for light to travel from one person to another several miles away. Their errors in timing would have been far greater than than the time they were attempting to measure.
The first reasonably accurate value was calculated by the Danish astronomer Ole Römer in 1676 (Figure 2). He noticed that Io, one of the moons of Jupiter, was blocked from Earth's view at certain intervals of time. These eclipses occurred when Io was behind Jupiter which stopped the light from reaching Earth. When Earth was nearest to Jupiter he calculated the times when he expected the eclipses to happen, but he found that when Earth was on the far side of the Sun the eclipses occurred some time later. He reasoned that the delay was due to the light take longer to travel the extra distance. As he knew the distance involved he was able to calculate the speed of light.
Another astronomical determination of the velocity was made by the English astronomer James Bradley in 1728. He observed that the stars are seen in slightly different directions depending on the position of Earth in its orbit. This phenomenon, called stellar aberration, is caused by Earth's motion and the differences in direction are simply related to the difference between this motion and the velocity of light. Bradley was therefore able to obtain a value for the velocity of light, and it was of the same order as Römer's figure.
It was until almost 200 years later that Römer's result was verified by the Frenchmen, Fizeau and Foucault. Fizeau in 1849, and Foucault in 1862, succeeded in measuring the speed of light using comparatively short light paths. Neither made use of astronomy.
Fizeau's method
Fizeau used a toothed wheel to help him measure the time taken for light to travel 12 miles (Figure 3). A converging lens gathered up the light rays from a powerful light source. A plate of glass was placed at an angle to these rays just before they would have been brought to a focus. Instead, the light rays were reflected and brought to a focus on one side of the glass plate. These rays were made parallel by a collimating lens placed so that the actual light focus coincided with the principal focus of the lens. The rays traveled in this parallel condition over a distance of about 6 mi before meeting yet another converging lens which brought them to a focus at a concave mirror placed so that the rays were reflected back along the same path and brought to a focus by the first lens just before the glass plate. They passed through the glass plate and the image they formed (at the focus of the first lens) was viewed by Fizeau using an eyepiece. Fizeau had a wheel carefully cut so that it had 720 teeth spaced equally round its rim. The spaces between the teeth were exactly the same size as the teeth themselves. The rim of the wheel was placed so that a tooth could block off the outgoing and returning light at the light focus. It was then rotated, first slowly and then faster and faster until no light image could be seen through the eyepiece, only darkness. Outgoing light was passing through a gap between the teeth. This light traveled the 6 miles to the mirror and another 6 miles back, during which time the next tooth had moved into the space, blocking the image from the viewer. As he knew the distances involved and the speed at which the wheel was rotating, it was an easy step to calculate the speed of light.
Foucault's method
Foucault's apparatus was much simpler than Fizeau's and the light was timed over a much shorter distance (Figure 4). This had the advantage that the space could be filled with water or other transparent substances to find how fast light traveled through them. The space could also be evacuated to find the speed of light in a vacuum. Light travels slightly more slowly in air than it does in a vacuum. It travels through water with only ¾ of its speed in air. It travels through glass with an even smaller speed. The actual speed depends on the type of glass used.
Light from the source passes through a plate of glass and then through a converging lens which concentrates it into the reflecting surface of a plane (flat) mirror. Another mirror, this time concave, is placed so that light reflected from the plane mirror is brought to focus on its surface and reflected back along the same path by which it came. But when the light reaches the plate of glass, although some of it passes through, some is also reflected by its surface in just the same way that a glass window can give a reflection. These reflected light rays converge forming an image of the light source. This image is viewed through an eyepiece. Now the plane mirror is set rotating as fast as it can be made to move. When the light it reflects falls back on it, the mirror is in a different position and consequently the image viewed through the eyepiece is slightly shifted. The light speed can be worked out from the speed of rotation, the extent of the shift, and the distances between the mirrors.
There are many modifications to this basic idea from which more accurate results have been found.
The largest error in Foucault's method lay in measuring the small shift made by the image. It would have been much better if he could have rotated the mirror so fast that it was back again in the same position to receive the returning light. This would give an image in the same position and only the speed of rotation and the distances between the two mirrors would be needed to calculate the speed of light. Michelson overcame this problem by replacing the plane mirror with a glass octagon. Different facets of the octagon reflected the light on both its outward and return journeys. Hence light could only reach the observer when the octagon was in one particular position. This would be the case if the octagon were stationary or if it were rotating at such a speed that one facet exactly replaced the next while the light was traveling over its measured path to a distant reflector and back again. The speed of rotation which fulfils this condition could be found accurately and used in calculating the speed of light.
Michelson's method
A rotating mirror was used by Michelson to measure the velocity of light in 1927 (Figure 5). Light traveled from one face of the mirror to a plane mirror 35 kilometers (22 miles) away and then back to another face and an eyepiece. An image of the light source was obtained with the mirror first stationary and then rotated at sufficient speed for the image to be seen in the same position. At such a speed the mirror turned so that the next face moved into position as the light made its 70-kilometer (44-mile) journey to and from the plane mirror. Velocity of light was calculated from the speed of rotation.
Mystery of the ether
Having determined that light has a certain velocity scientists began to wonder how light waves could travel through space. Other wave motion need a medium in which to travel – sound, for example moves through air – and light had to have a medium too.
As the medium through which light moved could not be seen to exist, one was invented; it was called the ether and it was supposed to pervade the whole universe. Thorny problems surrounded the ether. Known wave motions move more rapidly in denser, more elastic substances and a wave motion as fast as light should theoretically need a medium denser than steel. Yet the planets continue to sail through space, unimpeded by the ether. There were many other contradictions and so an experiment was made to detect the motion of Earth through the ether.
In the 1880s two American physicists, Albert Michelson (1852–1931) and Edward Morley (1838–1923), made a simple instrument to detect the ether (see Michelson-Morley experiment). In it a beam of light was split into two beams at right-angles and the two beams reflected from mirrors before recombining. Combined beams show interference effects if one travels a slightly longer path than the other. Michelson and Morley observed the combined beams in one direction and then turned the instrument at right-angles and observed the beams again. If the light were traveling in an ether it would have to move over a different path in the direction of Earth's motion from at right-angles to it. Turning the instrument at right-angles should show a difference in the interference effects if the ether existed. None was observed and none had been observed in many repeats of this classic experiment.
The basis of relativity
The conclusion of the Michelson-Morley experiment was that ether does not exist and light does not need a medium for its propagation, or that the ether can never be detected. Without a stationary ether there is no basis in the universe against which the absolute motion of everything can be measured, except for light. The Michelson-Morley experiment showed that the velocity of light is the same in the direction of Earth's motion as at right-angles to it and is always the same whatever the observer's motion. These conclusions had profound implications but to realize them it took a genius – Albert Einstein – who used them as a basis for the theory of relativity.
Faster-than-light travel
 |
Although Einstein's special theory of relativity insists that it is impossible to accelerate an object up to the speed of light and beyond (see light barrier), there has been no shortage of speculation on how ways may be found to circumvent this natural speed restriction. First, Einstein's theory allows in principle the creation of bizarre particles, known as tachyons, that have speeds permanently greater than that of light. Second, an object may be able to travel, apparently superluminally, between two far-flung points in the cosmos, providing it does not make the journey through conventional space-time. This opens up the possibility of using space-time gateways and tunnels, known as wormholes, as a means to circumvent the normal relativistic constraints.

