spacetime
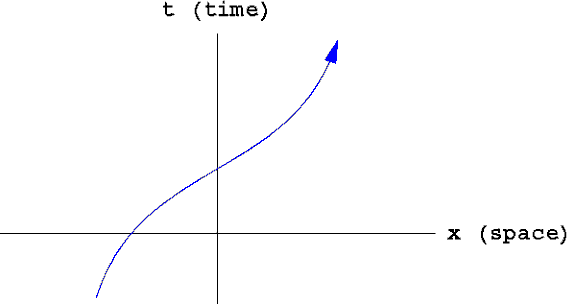
A worldline shown on a graph of space against time.
Spacetime is the union of space and time into a four-dimensional whole. More precisely, it is the inseparable four-dimensional manifold, or combination, which space and time are considered to form in the special and general theories of relativity. In the absence of a gravitational field, spacetime reduces to Minkowski space.
A point in spacetime is known as an event. Each event has four coordinates (x, y, z, t). Just as the x, y, z coordinates of a point depend on the axes being used, so distances and time intervals, which are invariant in Newtonian physics, may depend, in relativistic physics, on the reference frame of an observer; this can lead to bizarre effects such as length contraction and time dilation. A spacetime interval between two events is the invariant quantity analogous to distance in Euclidean space. The spacetime interval s along a curve is defined by the quantity
ds 2 = dx 2 + dy 2 + dz 2 - c 2dt 2
where c is the speed of light. A basic assumption of relativity theory is that coordinate transformations leave intervals invariant. However, note that whereas distances are always positive, intervals may be positive, zero, or negative. Events with a spacetime interval of zero are separated by the propagation of a light signal. Events with a positive spacetime interval are in each other's future or past, and the value of the interval defines the proper time measured by an observer traveling between them.
On ultramicroscopic scales, the quantum nature of spacetime would become apparent and require a quantum theory of gravity to describe it.
Worldline
A worldline is the history of a particle as represented on a spacetime (Minkowski) diagram (see illustration). The worldline of a particle is straight if the particle moves uniformly and is curved if it moves non-uniformly (i.e. if there is an acceleration). Rays of light can be treated as the worldlines of photons. The worldlines of particles under the influence of a gravitational field are geodesics in spacetime. The worldline of a photon near a star, such as the Sun, is slightly bent due to the light being deflected by the gravitational field of the Sun.
My Worldline is the title of the autobiography of George Gamow, the Ukrainian-American physicist.
Block universe
The block universe is a view of spacetime that affords equal (ontological) status to all points in spacetime, thus regarding temporality as an illusory human construct with no reference to reality as understood by modern physics.

