attractor
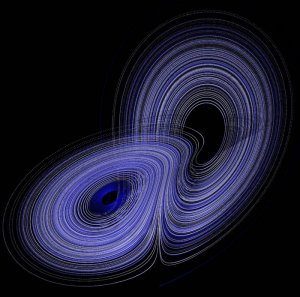
The Lorentz attractor: the best-known chaotic attractor.
An attractor is a trajectory, or set of points in phase space, towards which nearby orbits converge, and which is stable. Specific types of attractor include fixed-point attractor, periodic, and chaotic attractors, as described below.
Basin of attraction
The basin of attraction is the set of all points in phase space that are under the influence of an attractor, or, more generally, the initial conditions of a system that evolve into the range of behavior allowed by the attractor. If one imagines a complex system as a sink, then the attractor can be considered the drain at the bottom, and the basin of attraction is the sink's basin.
Types of attractor
Fixed-point attractor
A fixed-point attractor is an attractor that is represented by a particular point in phase space, sometimes called an equilibrium point. As a point it corresponds to a very limited range of possible behaviors of the system. For example, in the case of a pendulum, the fixed-point attractor represents the pendulum when the bob is at rest. This state of rest attracts the system because of gravity and friction.
Periodic attractor
A periodic attractor, also called a limit cycle attractor, is an attractor that consists of a periodic movement back and forth between two or more values. The periodic attractor represents more possibilities for system behavior than does the fixed-point attractor. An example of a period two attractor is the oscillating movement of a metronome or, in psychiatry, a bipolar disorder that causes a person's mood to shift back and forth from elation to depression.
Chaotic attractor
A chaotic attractor, also known as a strange attractor, is a type of attractor (i.e., an attracting set of states) in a complex dynamical system's phase space that shows sensitivity to initial conditions.


