chaotic attractor

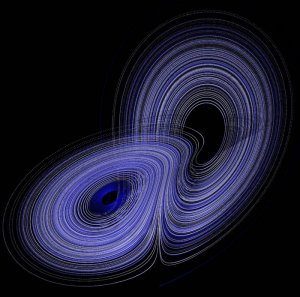
The Lorentz attractor: the best-known chaotic attractor

Also known as a strange attractor, a type of attractor (i.e., an attracting set of states) in a complex dynamical system's phase space that shows sensitivity to initial conditions. Because of this property, once the system is on the attractor nearby states diverge from each other exponentially fast. Consequently, small amounts of noise are amplified. Once sufficiently amplified the noise determines the system's large-scale behavior and the system is then unpredictable.

Chaotic attractors themselves are markedly patterned, often having elegant, fixed geometric structures, despite the fact that the trajectories moving within them appear unpredictable. The chaotic attractor's geometric shape is the order underlying the apparent chaos. It functions in much the same way as someone kneading dough. The local separation of trajectories corresponds to stretching the dough and the global attraction property corresponds to folding the stretched dough back onto itself. One result of the stretch-and-fold aspect of chaotic attractors is that they are fractals; that is, some cross-section of them reveals similar structure on all scales.

Related category

• CHAOS, COMPLEXITY, AND DYNAMICAL SYSTEMS

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP