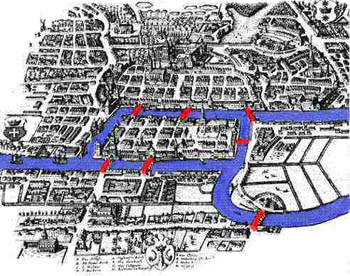
The Bridges of Königsberg is a famous routing problem that was analyzed and solved by Leonhard Euler in 1736, and that helped spur the development of graph theory. The old city of Königsberg, once the capital of East Prussia, is now called Kaliningrad, and falls within a tiny part of Russia known as the Western Russian Enclave, between Poland and Lithuania, which (to the surprise even of many modern Russians) is not connected with the rest of the country! Königsberg lay some four miles from the Baltic Sea on rising ground on both sides of the river Pregel (now the Pregolya), which flowed through the town in two branches before uniting below the Grune Brocke (Green Bridge). Seven bridges crossed the Pregel and connected various parts of the city, including Kneiphof Island, the site of Königsberg University and the grave of its most famous son, the great philosopher Immanuel Kant.

A question arose among the town's curious citizens: Was it possible to make a journey across all seven bridges without having to cross any bridge more than once? No one had been able to do it, but was there a solution? Euler, who was in St. Petersburg, Russia, at the time, heard about this puzzle and looked into it. In 1736 he published a paper called Solutio problematis ad geometriam situs pertinentis (The solution of a problem relating to the geometry of position) in which he gave his answer. Euler reasoned that, for such a journey to be possible, each land mass would need to have an even number of bridges connected to it, or, if the journey began at one land mass and ended at another then those two land masses alone could have an odd number of connecting bridges while all the other land masses would have to have an even number of connecting bridges. Since the Königsberg bridges violated this layout, a grand tour that involved only one crossing per bridge was impossible. Euler's paper was important because it solved not just the Königsberg conundrum but the much more general case of any network of points, or vertices, that are connected by lines, or arcs. What is more, the words "geometry of position" in the title shows that Euler realized that he was dealing with a different type of geometry where distance is irrelevant; so this work can be seen as a prelude to the subject of topology.