topology

Topology explores the properties of geometric shapes that have been deformed but not torn. If A1 and B1 are folded so that the arrows point in the same direction, a collar A2 and a twisted band B2 result. A2 has an inner and outer surface and two edges, but B2 has only one of each – precisely because of its twist. B2 is called a Möbius band and, unlike A2, a path beginning at S and traced round the band will, after one revolution, end on the other "side" of the band at T. A Möbius band stretched as in C1 is distorted further into one half of a Klein bottle (C2), which again has only one edge and one surface. Compare with a normal bottle (C3).
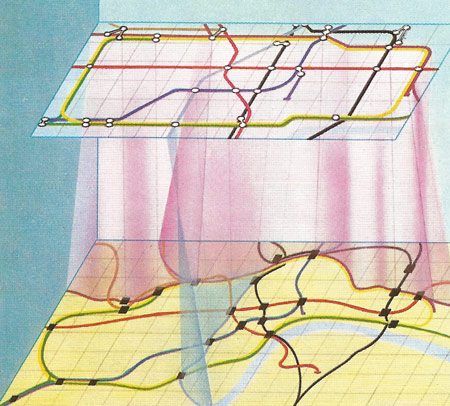
The London Underground map is a very distorted plan of the lines. But they correspond point-by-point, and two points joined on the map are connected in reality. This fundamental test makes them topologically identical.
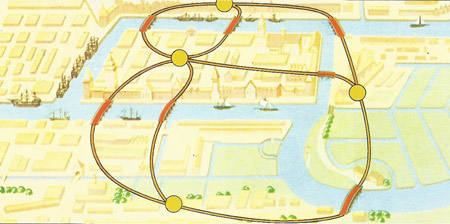
Königsberg, a Prussian town, posed a teaser that led to topological 'graph theory'. Could you take a stroll crossing each of the seven bridges only once? In 1734 the Swiss mathematician Leonard Euler analyzed the problem to form a theory of the traversability of a network or 'graph' (shown superimposed on the city). One bridge has to be crossed twice. The problem depends on connections, not distances.
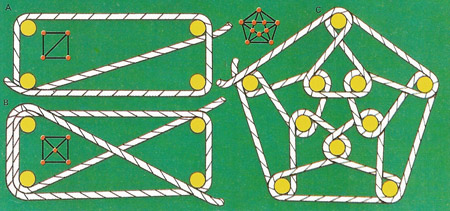
A graph traversable in one pass must have an even number of lines meeting at each junction. The pentagram C is traversable but the rope makes a double pass on rectangle B and begins and ends at different points on rectangle A.
A flat map needs no more than four colors to prevent adjacent areas sharing the same color. This theorem, which has now been proven correct, is part of graph theory, because every map can be drawn as a graph with areas as junctions and boundaries as lines.

On a donut, or torus, a map can need up to seven colors to prevent adjacent areas sharing the same color. The map shown (with its mirrored reflection for completeness) needs all seven because each area touches the other six. The sections form a continuous helix winding round twice before closing on itself.
Topology is the study of those properties of mathematical objects that remain unaffected by smooth deformations, such as stretching and squeezing, but that don't involve tearing.
The word comes from the Greek topos for "place," and was introduced into English by Solomon Lefschetz in the late 1920s.
A topologist has been described as someone who doesn't know the difference between a doughnut and a coffee cup. Substitute "care about" for "know" and this becomes more accurate.
Imagine a doughnut-shape, or torus, made of soft clay. A potter can easily shape this into a cup with a handle without removing or creating any new holes. Both shapes, in topology, are said to be genus 1 – objects with a single hole. A sphere, by contrast, is genus 0 (no holes), while an eyeglass frame, with the lenses removed, is genus 2.
Spheres, nets and knots
It is a topological truth that, regardless of its length or curvature, a hosepipe has two ends. Similarly, we feel sure that no matter what the size of a tablecloth, or the outline of a hole in it, it would be hard to spread the cloth out with the hole underneath. Topology takes such intuitive matters and formalizes them into mathematical logic. It is concerned with all those properties of objects that are unaffected by any change of form, however extreme. For instance, any simple solid object without holes is a "ball" to an topologist, for if made of deformable clay it could be rounded into a ball without being torn. Thus topology is sometimes called "rubber sheet geometry".
A button with four holes in it is not a topological ball. It is a "quadruply connected solid" because you would have to make four cuts in it, opening out the holes to the edge of the button, to make a shape that is a topological sphere. Small creatures living on the button would find it a different kind of space to the surface of a sphere. Any closed curve on a sphere, for example, must fence off and enclose a definite area. On a button this is not so. A closed curve round one of the holes does no such thing. The pure topologist's main concern is to decide whether particular abstract entities (objects or spaces of many forms and dimensions) are or are not topologically equivalent. Human intuition in comprehending the basic topology of even simple figures is relatively limited and sometimes leads to wrong conclusions.
This strange branch of mathematics has links with the real world. An electrical circuit is a topological entity, for example; its exact layout does not matter because only the pattern of interconnections is electrically significant. Graph theory, the branch of topology that handles networks, is fundamental in advanced circuit design. And the age-old crafts of knitting and weaving are really exercises in applied topology. A loop with a knot in it retains that knot however it is deformed and cannot be "undone"; it is topologically different from an unknotted loop. Textile manufacturers practise topology in their efforts to produce garments with specific topological properties; ones that can be knotted in one piece or that will not unravel if a fibre breaks.
A mathematical playground
Most serious topology has, as yet, little to do with the practical world. No branch of it is as closely tied to human affairs as, say, arithmetic is to banking. It is therefore a subject full of potential - for time and time again is the history of mathematics such theorists' playgrounds have become the workshops of a new science or discipline. At present, however, theorems in topology, although proved with full rigour, are less directly useful than those of a subject like geometry.
A typical topological theorem says that in coloring a flat map no more than four colors are ever needed to ensure that adjacent areas need not share the same color, The theorem does not state how this can be accomplished for any given case but merely asserts that it can always be done somehow. Similarly it is topologically certain that however briskly a cup of tea is stirred, at any instant at least one point in the liquid is not moving, The topologist is not concerned to identify this point; he just proves that it must exist. In different types of space different theorems hold good. There need by no fixed points in a stirred inner-tube full of water; on a doughnut, up to seven colors may be needed for a map without adjacent colors; and on a Mobius strip, up to six colors may be needed.
A Mobius strip is some sort of vindication of Monsieur Hulot for it is a contradiction of the strong human intuition that a piece of paper must have two sides. It is named after the German astronomer mathematician August Mobius. His strip can be made simply by cutting out a ribbon of paper, making a half turn in the middle of it and sticking the ends together to form a twisted loop. This loop now has only one side, as you can prove by drawing along it with a pen, never going over the edge until you meet your starting-point again. Cutting along the line creates another surprise.
Twisted space
Topologists study such "twisted spaces" in more dimensions than two, hard though they are to imagine. Indeed it is topologically entirely possible that the universe itself has a Mobius twist in it. One result of this might be that a traveler who went far enough out into space would return reversed in mirror-image fashion with his heart in the right side of his chest. Glove manufacturers might then be able to make only left-handed gloves and ship half their output around the universe from where they would return as matching right-handed ones.
For more on topologically intriguing structures, see Möbius band and Klein bottle.
Terms in topology
algebraic topology
A branch of topology that deals with invariants of a topological space which are algebraic structures, often groups.
cohomology
Cohomology is a subject that involves calculating algebraic invariants of topological spaces that are formally dual to homology. The invariants obtained are in general more powerful than those given by homology and usually have more algebraic structure. Generalized cohomology theories, both for topological spaces and for purely algebraic structures, have been developed that have some of the formal properties of cohomology but which don't have the same geometric background.
differential topology
A branch of topology concerned with those properties of differential geometry that are preserved by continuous transformation.
homology
Homology is a way of attaching Abelian groups, or more elaborate algebraic objects, to a topological space so as to obtain algebraic invariants. In a sense, it detects the presence of "holes" of various dimensions in the space. The methods developed to handle this led to what is now called homological algebra, a subject in which homological invariants are calculated for many purely algebraic structures.
point-set topology
Point-set topology, also known as general topology, is a branch of topology concerned with how to put a structure on a set in such a way as to generalize the idea of continuity for maps from the real numbers to itself. A topology on a set X is a certain set of so-called open subsets of the set X which satisfy various axioms. The set X together with this topology forms a topological space.
topological dimension
An integer that defines the number of coordinates needed to specify a given point of an object or set X. A single point therefore a topological dimension equal to zero; a curve has dimension one, a surface has dimension two, and so on.
topological space
A topological space is a type of generalized mathematical space in which the idea of closeness,
or limits, is described in terms of relationships between sets rather than in terms of distance. Every topological space consists of: (1)
a set of points; (2) a class of subsets defined axiomatically as open sets;
and (3) the set operations of union and intersection.
If a topological space is metrizable it means
that there exists a metric compatible with the topology. To say that a topological space
is metrizable is to treat it as a metric space, but without distinguishing
any specific or preferred distance function.

