The Möbius band is a simple, mathematically important, and wonderfully entertaining two-dimensional object, also known as the Möbius strip, that has only one surface and one edge and is therefore of great interest in topology. In particular, it is the starting point for creating non-orientable surfaces – those for which the concepts of right and left have no meaning. If a surface is non-orientable it must contain a Möbius band, and if a surface contains a Möbius band it must be non-orientable. The Möbius band also falls into the category of mathematical objects known as ruled surfaces.

 

Discovery

The band (or strip) is named after the German mathematician, pioneer of topology, and theoretical astronomer August Ferdinand Möbius (1790–1868), who discovered it in September 1858, although his compatriot and fellow mathematician Johann Benedict Listing (1808–1882) independently devised the same object in July 1858.

 

Construction, experiments, properties

 

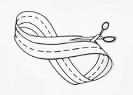
Making a Möbius band couldn't be easier: take an A4, or similar, sheet of paper, cut an 11" × 1" rectangle, bring the two long ends together, twist one of the ends through 180°, and tape the two ends together. To prove that the band is single-sided, take a pen and start drawing a line around the band's circumference. When drawing the line, never take the pen off the paper; just keep on going until you return to the starting point. Once you've finished, look all around the shape at the continuous line on it. This unbroken line proves there is just a single side because you never took the pen off the paper. (Hence the joke: "Why did the chicken cross the Möbius band? To get to the same side!")

 

If you now cut down this line with a pair of scissors, the result is surprising: a single long strip with a full 360° twist in it. This new shape is topologically equivalent to a cylinder (although it can't be manipulated into an ordinary cylinder because it is embedded differently in space).

 

 

As an experiment, try cutting around a Möbius band one-third of the way from the edge. What do you get? Make a collection of Möbius bands – fat ones. Mark them in fourths, fifths, sixths, and cut around them. Keep a record of your results.

 

Try experimenting further with the products of your experiments. For example, what happens if you cut down the middle of the long strip you get when you cut down the middle of a Möbius band? What happens if you start off with a (non-Möbius) band that has three half-twists and cut it down the middle, or a third the way from one edge? How many surfaces and edges do your creations have? Is there a pattern to the results so that you can easily predict what will happen to a given object sliced in a particular way?

 

A closely related strange geometrical object is the Klein bottle, which can be produced by gluing two Möbius bands together along their edges; however, this can't be done in ordinary three-dimensional Euclidean space without creating self-intersections.

 

Möbius band and 'bundles'

The Möbius band is the simplest example of what in topology is called a bundle. Despite its common or garden name, a bundle has a very technical definition in topology. It's a map between two topological spaces A and B, where the sets f ^–1(b) for elements b of B (known as fibers), are all homeomorphic to a single space. In the case of the Möbius band, A is the band, B is a circle, and the fibers are homeomorphic to an interval on the real number line.

 

Practical applications

The Goodrich Turnover Conveyor Belt System

 

In 1957, the B. F. Goodrich Company patented a conveyor belt that it went on to produce as the Turnover Conveyor Belt System. Incorporating a half-twist, it had the advantage over conventional belts of a longer life because it could expose all of its surface area to wear and tear. Möbius belts are no longer manufactured because untwisted modern belts can be made more durable by constructing them from several layers of different materials.

 

Other practical applications of Möbius bands have included half-twisted, continuous-loop recording tapes (to double the playing time), typewriter ribbons, and computer printer cartridges. In the 1960s Sandia Laboratories used Möbius bands in the design of versatile electronic resistors. Also there have been a number of ideas for children's toys based on the shape, including a railway in which a miniature engine traverses a three-dimensional looped track using magnets to hold on while it travels some of the sections upside-down.

 

Möbius band in art and sculpture

M. C. Escher famously used the Möbius band as the basis for a number of his lithographs including Möbius Strip II (1963) shown here. American physicist and artist Robert Rathbun Wilson (1914–2000) was also fascinated by the shape. "Möbius Strip" is among several of Wilson's sculptures that grace the grounds of the Fermi National Accelerator Laboratory (Fermilab) in Batavia, Illinois. This 8-ft-diameter, three-dimensional version of the loop with a half-twist stands in the middle of a circular pool atop the Norman F. Ramsey Auditorium in front of the Fermilab's largest building – Wilson Hall.

 

Escher's Möbius Strip II (1963). Collection Haags Gemeentmuseum, The Hague

 

Möbius band in psychoanalysis

Topology and the nature of the self would seem to be very disparate subjects. Yet the French psychoanalyst Jacques Lacan was able to draw a connection. Lacan argued that we tend to think of the self by analogy with the body: clear outlines, and a clear division between inside and outside. He used topological models such as the Möbius band and self-intersecting surfaces to suggest that things may be a good deal more complex than that.

 

Möbius bands, the universe, and everything

In his book Art & Physics: Parallel Visions in Space, Time, and Light, Leonard Shlain remarks on the cosmic symbolism of the Möbius band and how it was employed by Escher in this context.³ Shlain points to the seemingly distinct natures of space and time which are like the two different sides of spacetime. "But," says Shlain, the distinction, like the apparency of opposing surfaces on the Möbius strip, is an illusion. When followed out to their own ends, both sides meet in one seamless, endless, recursive continuum." Shlain goes on to argue that the Möbius band is a visual repudiation of Aristotle's claim that extremes cannot be brought together via an excluded middle.

 

Möbius band in science fiction

In "A Subway Named Möbius" (1950), A. J. Deutsch imagines a train line that has become so complex and convoluted that one of the trains on it disappears into another dimension. The mathematical connection with a Möbius band is tenuous but the story is nevertheless intriguing and memorable.

 

Martin Gardner's "No-Sided Professor" tells of a mathematician who invents a folding that goes one step beyond Möbius and creates an object with zero sides!

 

Perhaps the most striking of all science fiction stories that use the Möbius theme is Arthur C. Clarke's "The Wall of Darkness" (1946). A mysterious, impenetrable wall runs all the way around a planet, in a universe in which this world and its sun are the only objects. Two men, one with money, the other with building skills, determine to scale the wall and discover what's on the other side. What they find is both Möbian and rather unsettling.

 

Other

	Möbius chess is played on a board that is taken to be a Möbius band. Lengthwise the board is continuous and endless, incorporating the familiar half-flip; however, the width is only four squares. An unusual consequence of this set up is that bishops lack fixed colors.
	Mobius Band is a electronic rock trio originally from western Massachusetts, now living in Brooklyn. The band's first album is called The Loving Sounds of Static.
	The Möbius band has become the universal symbol of recycling. The symbol was devised in 1970 by Gary Anderson, who, at the time was a senior at the University of Southern California, as part of a contest sponsored by a paper company.

 

References

1. Gardner, Martin. Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleights-of-Mind from Scientific American. New York: Vintage, 1978.
2. Pickover, Clifford A. The Möbius Strip: Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. Thunder's Mouth Press, 2006.
3. Shlain, Leonard. Art & Physics: Parallel Visions in Space, Time, and Light. New York: William Morrow & Company, 1991.