circle

Figure 1. To find the equation of a circle, observe that each point on it forms a right-angled triangle whose sides are the x distance and y distance and whose hypotenuse is r. Pythagoras's theorem tells us that x 2 + y 2 = r 2. For points outside the circle x 2 + y 2 exceeds r 2; inside it x 2 + y 2 is less than r 2. Along the intersection of these two regions the equation balances. All mathematical curves divide space in this way.

Figure 2. Terms associated with a circle.
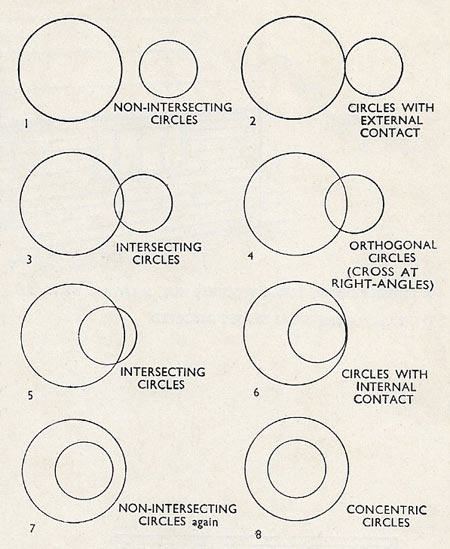
Figure 3. Different positions of two circles. The figures show various stages of one circle moving towards another, with the names describing the relation between the circles.
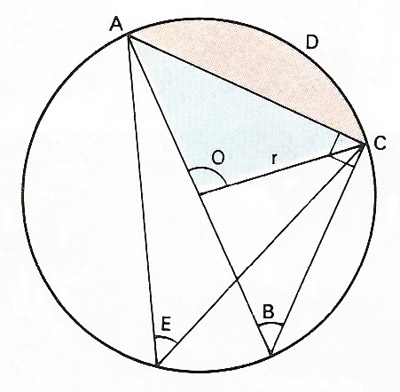
Figure 4. Inscribed angles of a circle.
A circle is the set of all points in a plane at a given distance r, called the radius, from a fixed point, called the center. A circle is a simple closed curve that divides the plane into an interior and exterior. It has a perimeter, called a circumference, of length 2πr, and encloses an area of πr 2.
In coordinate geometry a circle with center (x0, y0) and radius r is the set of all points (x, y) such that:
(x - x0) 2 + (y - y0) 2 = r 2.
If the center is at the origin (0, 0), as in Fig 1, then this equation reduces to
x 2 + y 2 = r 2
'Circle' comes from the Latin circus, which refers to a large round or rounded oblong enclosure in which the famous Roman chariot races were held.
A line cutting a circle in two places is called a secant. The segment of a secant bound by the circle is called a chord, and the longest chord is that which passes through the center and is known as a diameter. The ratio of the circumference to the diameter is π. The length of a circle between two radii is called an arc; the ratio between the length of an arc and the radius defines the angle between two radii in radians. The area bounded by two radii and an arc is known as a sector.
A segment is part of a circle bounded by a chord and the arc subtending the chord. A line touching a circle in one place is called a tangent. Tangent lines are perpendicular to radii. Figure 2 illustrates the different parts of a circle. Figure 3 shows what circles are called in different relationships to each other.
In affine geometry all circles and ellipses become congruent, and in projective geometry the other conic sections join them. A circle is a conic section with eccentricity zero. In topology all simple closed curves are homeomorphic to circles, and the word circle is often applied to them as a result. The three-dimensional analog of the circle is the sphere, and the four-dimensional analog is the hypersphere.
Circle theorems of Euclid
16th theorem
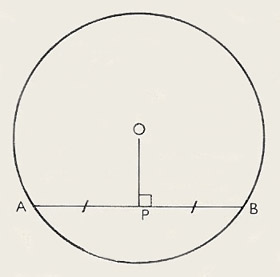 |
| O is the center of the circle. AB is a chord. OP is perpendicular to AB. The theorem tells us that P is the mid-point of AB.
|
The perpendicular onto a chord from the center of the circle bisects the chord.<
17th theorem
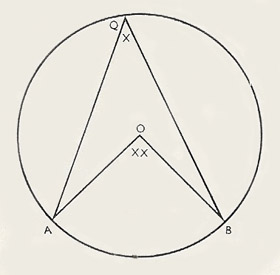 |
| A and B are any two points on the circle. O is the center. Q is any point on the circle. The angle at Q, marked x, is "the angle at the circumference". The angle at O , marked xx, is "the angle at the center". It is twice as large as the angle x.
|
The angle at the center is double the angle at the circumference.
18th theorem
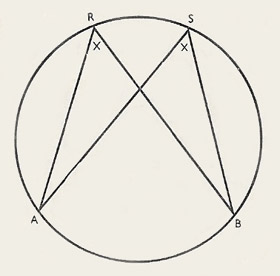 |
| A, B, R, and S are four points on the circle. The theorem says that the angles marked x are equal. Note that R and S must be between A and B, so that the order is ARSB or ARBS. If the order were ARBS, theorem 19 would apply instead.
|
Angles in the same segment are equal.
19th theorem
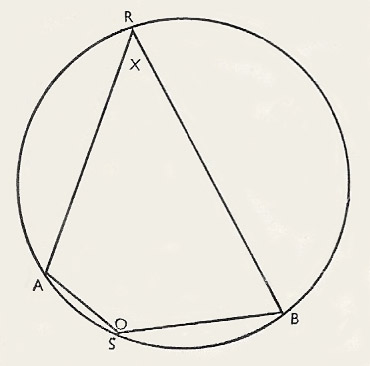 |
| The angles marked x and o and add to 180 degrees,
|
The opposite angles of a cyclic quadrilateral add up to 180 degrees.
20th theorem
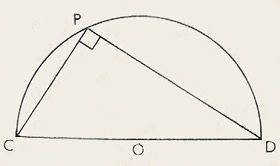 |
| O is the center of a circle. CD is a straight line through OThe angle in a semicircle is a right angle.
|
The angle in a semicircle is a right angle.
21st theorem
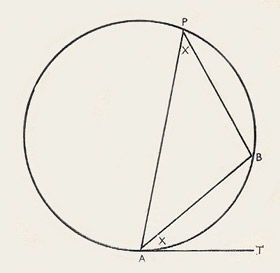 |
| A and B are any two points on the circle. AT is a tangent. P is a point on the circle.
|
This theorem deals with the "angle in the alternate segment" (see diagram).
22nd theorem
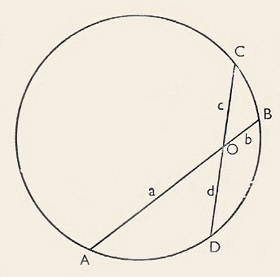 |
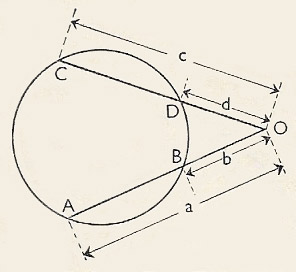 |
| This theorem deals with the products of parts of intersecting chords. A, B, C, and D are points on a circle. AB crosses CD at O. The theorem states that AO.OB = CO.OD (top illustration). If we use a, b, c, and d to stand for the lengths shown, we may write the result as: ab = cd. If the lines AB and CD meet outside the circle (lower illustration), the result AO.OB = CO.OD still holds.
|
23rd theorem
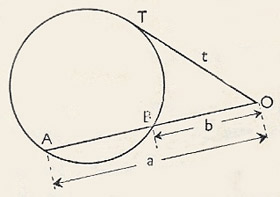 |
| This is a special case of theorem 22. If, in the lower illustration of theorem 22, C and D had been very close to each other, then we would effectively have the situation shown here. (C and D have met at the point T.) c and d have both become equal to t, so that ab = t2. The result holds when the line AB cuts the circle, and the line TO touches the circle at T.
|
Other circle theorems
Butterfly theorem
The butterfly theorem may be stated as follows: Let M be the midpoint of a chord PQ of a circle, through which two other chords AB and CD are drawn. If AD intersects PQ at X and CB intersects PQ at Y, then M is also the midpoint of XY. The theorem gets its name from the shape of the resulting figure.
Inscribed angle theorems
Referring to Figure 3, angle O = 2B = 2E. The general theorem that follows from this is that an inscribed is half the central angle. Also, B = E. In general, angles subtended by the same arc are equal.
Note, by the way, that the circumference of the arc ADC is πrO/180.
Johnson's theorem
If three congruent circles all intersect in a single point, then the other three points of intersection will lie on another circle of the same radius. This simple little theorem was discovered by Roger Johnson in 1916.
Nine-point circle
Draw a triangle, any triangle (although it may be best to start with an acute triangle). Mark the midpoints of each side. Drop an altitude from each vertex to the opposite side, and mark the points where the altitudes intersect the opposite side. (If the triangle is obtuse, an altitude will be outside the triangle, so extend the opposite side until it intersects.) Notice that the altitudes intersect at a common point. Mark the midpoint between each vertex and this common point. No matter what triangle you start with, these nine points all lie on a perfect circle! This result was known to Leonhard Euler in 1765, but was rediscovered by the German mathematician Karl Feuerbach (1800–1834) in 1822.
Six circles theorem
Given a triangle and a circle inside it that touches two of the triangle's sides, draw a second circle touching another two sides and touching the first circle. Draw a third circle touching two sides and the second circle, and so on. This chain ends with the sixth circle, which will touch the first.
Inscribed circle
An inscribed circle is a circle inside a triangle or other polygon whose edges are tangents to the circle. Such a polygon is said to be circumscribed (see circumscription) to the circle. The (unique) circle inscribed to a triangle is called the incircle.
Circle involute
A circle involute (Figure 5) is the simplest kind of spiral to draw and understand. It is, for example, the path that a goat, tethered to a post, would follow if it walked around and around in the same direction, keeping its tether taut until it wound its way to the center.
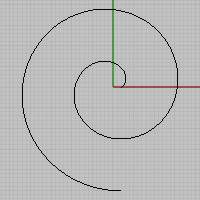 |
| Figure 5. Circle involute
|
The radial distance between adjacent loops of the spiral is equal to the circumference of the central circle. Except for the innermost loop, the circle involute is hard to distinguish from the Archimedean spiral, though the two curves are never identical.

