trigonometric function

Figure 1. The graph of y = cos x, for angles between 0 and 360 degrees.
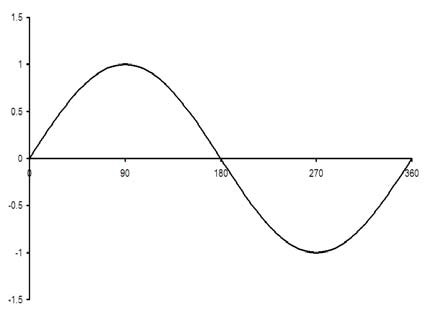
Figure 2. The graph of y = sin x, for angles between 0 and 360 degrees.
A trigonometric function is any of the functions sine (sin), cosine (cos), tangent (tan), secant (sec), cosecant (cosec), or cotangent (cot), or their inverses, sin–1, etc., which deal with certain proportions in right-angled triangles. The plane curve generated by a trigonometric function is called a trigonometric curve.
Cosecant
The cosecant function, cosec α, is the ratio of the hypotenuse (the longest side of a right-angled triangle) to the side opposite the angle α in a right-angled triangle, and equals 1/sin α.
Cosine
The cosine function, cos α, is the ratio of the side adjacent to the angle α to the hypotenuse in a right-angled triangle (Figure 1).
Cosine rule or theorem
The cosine rule or theorem may refer to any of three theorems:
The cosine theorem of plane trigonometry
This states that if a, b, and c are the sides, and α, β, and γ the angles of a triangle, then:
a 2 = b 2 + c 2 – 2bc cos α
b 2 = c 2 + a 2 – 2ca cos β
c 2 = a 2 + b 2 – 2ab cos γ
i.e., the square of any one side is equal to the sum of the squares of the other two sides less twice the product of those sides and the cosine of the angle they include. The cosine theorem of plane trigonometry can be used to solve a triangle if the three sides of the triangle are given or if two sides and the included angles are given.
The angle cosine theorem of spherical trigonometry
This states that if a, b, and c are the sides, and α, β, and γ the angles of a spherical triangle, then:
cos α = – cos β cos γ 2 + sin β sin γ cos a
cos β = – cos γ cos α 2 + sin γ sin α cos b
cos γ = – cos α cos β 2 + sin α sin β cos c
The cosine theorem for the sides of a spherical triangle
This states that if a, b, and c are the sides, and α, β, and γ the angles of a spherical triangle, then:
cos a = – cos b cos c 2 + sin b sin c cos α
cos b = – cos c cos a 2 + sin c sin a cos β
cos c = – cos a cos b 2 + sin a sin b cos γ
The angle cosine theorem can be used if three angles of a spherical triangle are given, or if one side and the two adjacent angles are given. The cosine theorem for the sides of a spherical triangle can be used if three sides or two sides and the included angle are given.
Cotangent
The cotangent is the ratio of the length of the side adjacent to an acute angle to the length of the side opposite the angle in a right-angled triangle. The cotangent of angle A is usually abbreviated cot A and is the reciprocal of the tangent.
Secant
In trigonometry, secant is the ratio of the length of the hypotenuse (the longest side) to the length of the side adjacent to an acute angle in a right-angled triangle. The secant of angle A is usually abbreviated to sec A, and is equal to the reciprocal of its cosine, that is 1 / cos A.
A secant is also a straight line that meets a curve in two or more points.
Sine
The sine function, sin a, is the ratio of the opposite side to the hypotenuse in a right-angled triangle.
For the graph of y = sin x, shown in the diagram, if the x-axis is extended, the graph repeats itself every 360°, i.e. the period is 360°. The amplitude oscillates between +1 and –1.
The sine rule or theorem
In plane geometry, if a, b, and c are the sides, and A, B, and C the angles of a triangle, then a : b : c = sin A : sinB : sin C. In other words:
a/sin A = b / sin B = c / sin C.
The theorem can be used to solve a triangle if one side, the opposite angle, and a further side or a further angle are given.
In spherical geometry, if a, b, and c are the sides, and A, B, and C the angles of a spherical triangle, then sin a : sin b : sin c = sin A : sinB : sin C. In other words:
sin a / sin A = sin b / sin B = sin c / sin C.
The sine theorem of spherical geometry, like that of plane geometry, can be used to solve a spherical triangle if one side, the opposite angle, and a further side or a further angle are given.
Tangent
In a right triangle, if one of the angles is θ, then the tangent of θ is the ratio of lengths of the side opposite θ to the side next to θ.
A tangent is also a straight line that touches a given curve exactly once, at a given point. The gradient of the tangent is equal to the instantaneous gradient of the curve at the point of contact.


