function
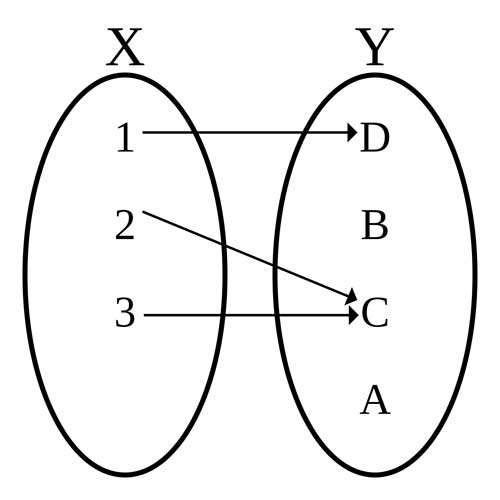
Diagram of a function, with domain X = {1, 2, 3} and codomain Y = {A, B, C, D}, which is defined by the set of ordered pairs {(1, D), (2, C), (3, C)}.
A function is a way of expressing the dependence of one quantity on another quantity or quantities. Each of its input values gives back one and only one output value. Often it is denoted as f (x), where x is the value given to it. For example, where the number x relates to its square x 2, the output of function f corresponds to input x and is written f (x). So if the input variable, or argument, is –4 then the output is 16 written as f (–4) = 16.
Traditionally, functions were specified as explicit rules or formulas that converted some input value (or values) into an output value. If f is the name of the function and x is a name for an input value, then f (x) denotes the output value corresponding to x under the rule f. An input value is also called an argument of the function, and an output value is called a value of the function. The graph of the function f is the collection of all pairs (x, f x)), where x is an argument of f.
For example, the circumference C of a circle depends on its diameter d according to the formula C = πd; therefore, one can say that the circumference is a function of the diameter, and the functional relationship is given by C(d) = πd. Equally well, the diameter can be considered a function of the circumference, with the relationship given by d(C) = d/π.
Again, if y = ax 2 + bx + c, where a, b, and c are constants, and x and y are variables, then y is said to be a function of x, since, by assigning to x a series of different values, a corresponding series of values of y is obtained, showing its dependence on the value given to x. For this reason, x is termed the independent variable and y the dependent variable.
There may be more than one independent variable – e.g. the area of a triangle depends on its altitude and its base, and is thus a function of two variables.
History
Galileo was the first to articulate the dependency of one quantity on another in mathematics. However, it was German philosopher and mathematician Gottfried Leibniz who introduced the word "function" into mathematics in his manuscript Methodus tangentium inversa, seu de functionibus (The Inverse Method of Tangents, or On Functions 1673), Leibniz used "function" to describe any quantity varying from point to point on a curve, such as the length of the tangent.
In 1692 and 1694, Leibnizpublished articles in which he named any parts of straight lines as "functions". In 1694, in a piece for the scientific journal AtaEruditorum (Acts of the Scholars), Swiss mathematician Jacob Bernouilli (1654–1705) used the word "function" to have the same sense. The notation f (x) was introduced in 1734 by Leonhard Euler. German mathematician Peter Dirichlet came up with the modern definition of "function" in 1837.
Types of function
Functions are primarily classified as algebraic or transcendental. The former include only those functions which may be expressed in a finite number of terms, involving only the elementary algebraic operations of addition, subtraction, multiplication, division, and root extraction.
Functions are also distinguished as continuous or discontinuous. Any function is said to be continuous when an infinitely small change in the value of the independent variable produces only an infinitely small change in the dependent variable; and to be discontinuous when an infinitely small change in the independent variable makes a change in the dependent variable either finite or infinitely great. All purely algebraic expressions are continuous functions, as are also such transcendental functions as ex, log x, and sin x.
Harmonic and periodic functions are those whose values fluctuate regularly between certain assigned limits, passing through all of their possible values, while the independent variable changes by a certain amount known as the period. Such functions are of great importance in many branches of mathematical physics. Their essential feature is that, if f (x) be a periodic function whose period is a, then f (x + ½a) = f (x – ½a), for all values of x.
Modern view of functions
In modern mathematics, the insistence on specifying an explicit effective rule has been abandoned; all that is required is that a function f associate with every element of some set X a unique element of some set Y. This makes it possible to prove the existence of a function without necessarily being able to calculate its values explicitly. Also, it enables general properties of functions to be proved independently of their form. The set X of all admissible arguments is called the domain of f; the set Y of all admissible values is called the codomain of f. We write f : X →Y.


