set

Figure 1a. Two families – one with three children and one with two – together make up a universal set. It can be represented diagrammatically as shown.
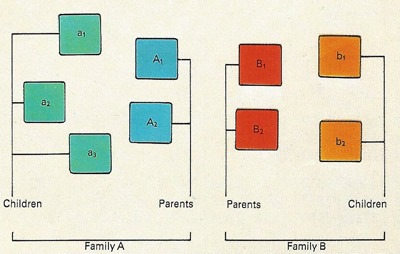
Figure 1b. In this diagram of the families in the top picture, letters have been given to each of the elements in the set. The letters are then sufficient for the mathematical manipulation of of the set in what are called Venn diagrams, first introduced by the mathematician John Venn in 1880. In such diagrams, areas represent sets of things.
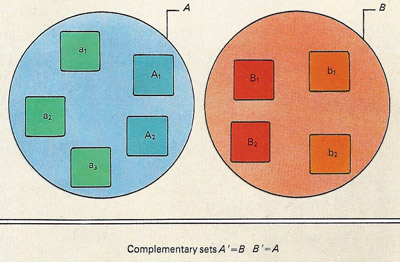
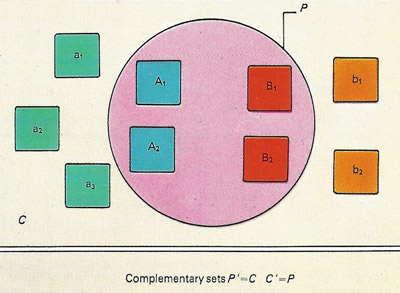
Figure 2. The above two Venn diagrams show how the universal set of illustration 1b can be split into two non-overlapping subsets. Each family can make up a subset (upper illustration) or the parents and children can each form subsets (lower illustration). In each case the subsets are complementary to each other because they include between them all the elements of the first universal set. The complementary relationships in the upper picture, for example, are written as A' = B and B' = A.
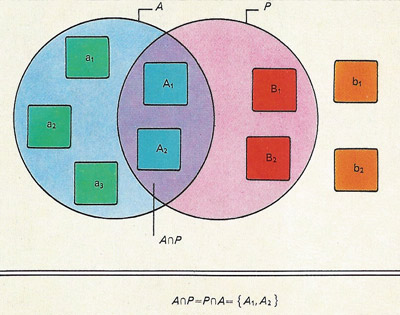
Figure 3. Intersection of sets generates another of subset that contains all the elements common to both. Here the intersection of A and P (written as A∩P) gives a subset containing only A1 and A2.
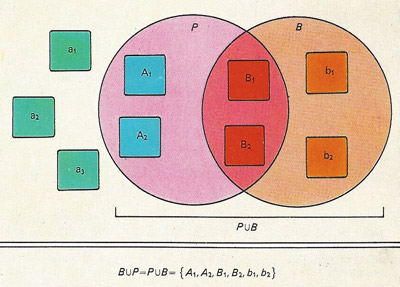
Fugure 4. The union of sets generates yet another subset that contains all the elements in the two original sets, in this example B and P. It is written B∪P and contains the elements A1, A2, B1, B2, b1, and b2. B∪P = P∪B illustrates the commutative law.
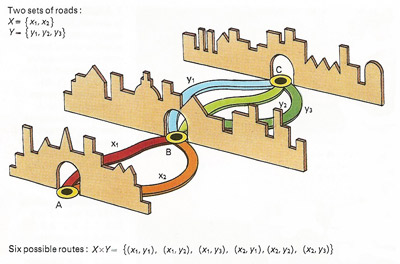
Figure 5. A map shows the roads connecting two towns A and C. All the roads pass through town B. The two routes from A to B are one set and the three between B and C another set. There are six possible ways of going between A and C. This is known as the Cartesian product of two sets, in this case all possible combinations of paired elements, taking one from each set. The study of networks is one aspect of the subject of topology.
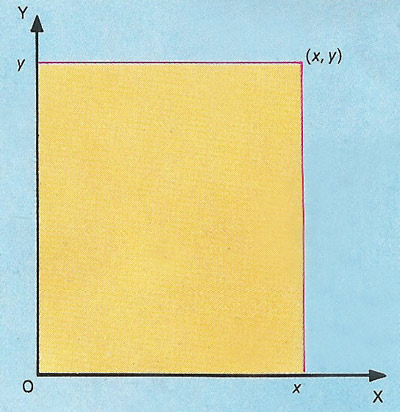
Figure 6. A plane defined by two lines is related to the Cartesian product of two sets that represent an infinite number of points on the lines. The point at the corner of the plane is defined by the coordinates x and y, written (x, y). These are called Cartesian coordinates and are used in coordinate, or analytic, geometry in which all lines, whether straight or curved, can be expressed in terms of algebraic equations.
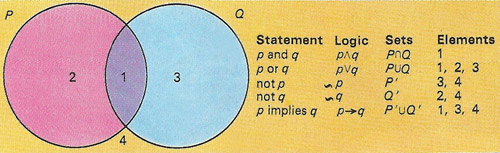
Figure 7. Union and intersection in set theory correspond to "or" and "and" in logic. This relationship enables particular elements and combinations of elements from sets to be defined by logical statements.
A set is a finite or infinite collection of objects known as elements. Sets are one of the most basic and important concepts in mathematics. An example of a finite set is the set of whole numbers from 1 to 58; an example of an infinite set is the set of all the rational numbers. Two sets are equal if, and only if, they contain the same objects.
The mathematical theory of sets (see set theory) was first investigated by Georg Cantor and later systematized by Ernst Zermelo (1871–1956), but the basic concepts were known earlier.
Standard set notation uses braces around the list of elements, as in: {red, green, blue}. If A and B are two sets and every x in A is also contained in B, then A is said to be a subset of B. If A and B are two sets and every x in A is also contained in B, then A is said to be a subset of B. Every set has as subsets itself, known as the improper subset, and the empty set.
Union and intersection
The union of a collection of sets S = {S1, S2, S3, ...} is the set of all elements contained in at least one of the sets S1, S2, S3, ... The symbol used to denote the union of two sets is the cup, ∪.
The intersection of a collection of sets T = {T1, T2, T3, ...} is the set of all elements contained in all of the sets. The symbol used to denote the intersection between two sets is the cap, ∩. Thus the intersection between sets P and Q is written as P ∩ Q. This is illustrated in a Venn diagram as the region of overlap between two sets. The cap was first used as the symbol for intersection by Guiseppe Peano in Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann (1888).
Collecting objects together
The concept of a set is one of the most fundamental in mathematics. A set is a collection of objects with a common description or definition, listed in any order according to a formal law. The set of oceans, for example, is defined as: oceans = {Pacific, Atlantic, India, Arctic, Antarctic} or O = {x | x is an ocean}. The letter O labels the set; x is called a variable; { and } are called braces; and the symbol | means "where" or "such that". This kind of set is a finite set because its cardinality (number of elements) – it has a known value, in this case in 5. The set of counting numbers is an infinite set because we cannot exactly how many elements it has: counting numbers = {1, 2, 3,...}, or C = {x | x is a counting number}.
The set of natural numbers is J+ = {1, 2, 3,...}, with the same elements as the set of counting numbers. We say that C and J+ are equal sets. Sets with the same cardinality are called equivalent sets: the set {blue, green, yellow, orange, red} is equivalent to the set of oceans – they each have five elements.
The language of sets can be understood by studying a particular example. A universal set (Figures 1a and 1b), the set of all elements under consideration, can be partitioned into what are called disjoint sets – that is, non-overlapping sets. If there are only two such sets, one is the complement of the other (Figure 2). The set of elephants living at the North Pole is an example of the empty or null set, since it has no elements. The null set is written as ø. The concepts of partition, complement, intersection (Figure 3), and union (Figure 4) are fundamental to the processes of classification of information.
Networks (Figure 5) give rise to the Cartesian product of two sets. This is obtained by finding all possible ordered pairs of elements, taking one from each set.
The word Cartesian is derived from René Descartes, who propounded the concept of coordinates. If set X is associated with the infinite set of points making one line in a plane and set Y is associated with the infinite set of points making another intersecting line, the Cartesian product of X and Y is associated with the infinite set of points making the plane containing the two lines (Figure 6).
Boolean and propositional algebra
The algebra of sets is known as Boolean algebra. It is isomorphic – that is, it has a one-to-one correspondence – with the algebra of propositions or logic. It is named after George Boole, who founded the modern study of logic. The two types of logic use different symbols, with union (∪) and intersection (∩) corresponding to or (∨) and and (∧). Propositional algebra analyses the sets of logical possibilities in which various statements and combinations of the statements are either true or false.
A mathematical system is created when one or more binary operations are applied to a set of elements. A binary operation combines two elements into a third of the same set. One of the most valuable systems is the group as it occurs in many diverse situations and helps to unify the study of mathematics.
Types of set
Countable set
A countable set is a set that is either finite or countably infinite. A countably infinite set is one that can be put in one-to-one correspondence with the natural numbers and thus has a cardinal number ("size") of aleph-null. Examples of countable sets include the set of all people on Earth and the set of all fractions.
Empty set
An empty set is the set, denoted by Ø or {}, that has no members; also known as the null set. This is not the same as zero, which is the number of members of Ø. Nor is Ø the same as nothing because a set with nothing in it is still a set, and a set is something. The empty set, for example, is the set of all triangles with four sides, the set of all numbers that are bigger than 9 but smaller than 8, and the set of all opening moves in chess that involve a king. Applying the concept of the empty set helps distinguish between the different ways that "nothing" is used in everyday language. In his book What Is the Name of This Book? (1978),1 Raymond Smullyan wrote:
Which is better, eternal happiness or a ham sandwich? It would appear that eternal happiness is better, but this is really not so! After all, nothing is better than eternal happiness, and a ham sandwich is certainly better than nothing. Therefore a ham sandwich is better than eternal happiness.
What is wrong with this? The first statement is equivalent to "The set of things that are better than eternal happiness is Ø." The second statement is equivalent to "The set {ham sandwich} is better than the set Ø." The confusion arises because the first is comparing individual things, while the second is comparing sets of things, and Ø plays a different role in each.
Reference
1. Smullyan, Raymond M. What is the Name of This Book? The Riddle of Dracula and Other Logical Puzzles. Englewood Cliffs, NJ: Prentice Hall, 1978.
Power set
The set of all subsets of a set X is called its power set and is denoted 2X or P(X).
Recursively enumerable set
A recursively enumerable set is a potentially infinite set whose members can be enumerated by a universal computer; however, a universal computer may not be able to determine that something is not a member of a recursively enumerable set. The halting set is recursively enumerable but not recursive.
Subset
A subset is a set whose members are members of another set; a set contained within another set.
Uncountable set
An uncountable set is a set of numbers that can't be put in a definite order from smallest to largest and so can't be counted. All uncountable sets are infinite, but not all infinite sets are uncountable. The best known uncountable set is the set of all real numbers. By contrast the set of all natural numbers, which represents the "smallest" type of infinity, is countable.
Universal set
A universal set is a set containing all the elements with a certain property. It is also the name given to a hypothetical set which could include everything. Such an all-encompassing set contradicts the basic notion of a set.


