group

Figure 1a. Four dancers, starting at the corners of a square, can have various positions as shown in the diagram below.
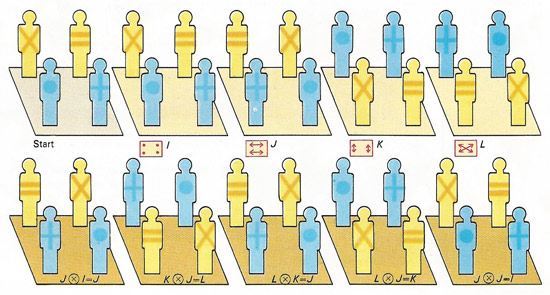
Figure 1b. The various positions of the dancers at the corners of a square can be represented by the symbols I, J, K, and L. Carrying out a pair of movements, one after the other, results in new positions (lower diagram) described as J follows I, for example. Sequences of three movements can be analyzed as two and the final position predicted. L follows K follows J, for example, reduces to L follows L, equals I.
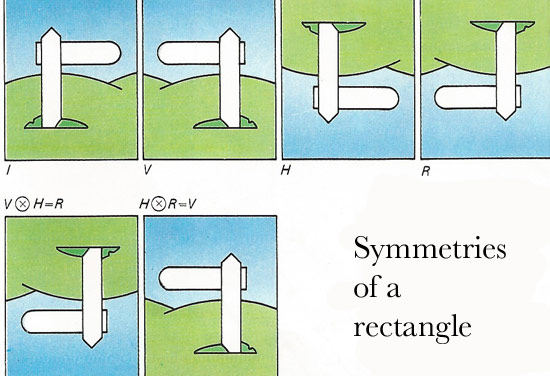
Figure 2. Symmetries of a rectangle involve rotating it in various ways – vertically V, horizontally H, or in the plane of the picture R. The letter I represents its original position. Again successive pairs of movements always result in one of the four.
Wherever groups disclosed themselves, or could be
introduced, simplicity crystallized out of comparative chaos.
—Eric Temple Bell
A group is an abstract and crucially important way of representing symmetry and one of the most fundamental concepts in modern algebra. A group is a set whose elements are defined by a single operation. The group is called additive if the symbol for the operation is "+" and is called multiplicative if the symbol "×" of multiplication is used instead. But any other symbol can be substituted for these. There is always a unique element (1, for multiplicative, and 0, for additive, groups) that leaves elements unchanged under the defined operation, like a + 0 = a. Also, for every element a there exists a unique inverse b such that, for example, in the case of the additive symbol, a + b = 0 and b + a = 0. Most often, however, the inverse is denoted as a-1. Lastly, the group operation must be associative as in a × (b × c) = (a × b) × c. A group is commutative or Abelian if its operation is symmetric, as in a + b = b + a.
Examples of groups
The concept of a group can be illustrated by studying a simple case of formation dancing (Figures 1a and 1b) in which dancers change their positions (or remain still) to form various patterns. The movements form the set and the operation is a combination of movements called "follows", indicated mathematically by the symbol ⊗. Combining any two movements results in one of the four. The identity element is I and each element is its own inverse in this particular example. We have the relationships (J ⊗ K) ⊗ L = L ⊗ L = I and J ⊗ (K ⊗ L) = J ⊗ J = I, so that the associative law (J ⊗ K) ⊗ L = J ⊗ (K ⊗ L) is valid. In the particular example of dancing there is another law, the commutative law: A ⊗ B = B ⊗ A.
From the four possible choices available in moving a rectangle [see illustration 2], a set of four transformations arises. These can be paired by the operation "follows" to produce a combination of movements that is in a one-to-one correspondence to those in the dancing example. The two type are said to be isomorphic. The search for isomorphisms is essentially the core of mathematical study.
Usefulness of group theory
Group theory is useful in the study of number systems. The set of integers (whole numbers) with 0 included, {... –3, –2, –1, 0, 1, 2, 3, ...}, is a group under addition with 0 as the identity element. The set of rational numbers is a group under addition if 0 is included. It is a group under multiplication if 0 is excluded. The use of group theory in the study of arithmetic not only enriches it but leads to higher concepts such as those of rings and fields, sets of elements subject to two binary operations (addition and multiplication) that satisfy certain axioms.
History of groups
Groups were brought into mathematics in the early nineteenth century by the radical young French student Évariste Galois as a tool to help solve one of the outstanding problems of his day: to find a formula for solving polynomial equations of order five – quintics – and higher. Galois showed, in notes scribbled down the night before he died in a duel, that no such formula exists. The reason for this is that the possible symmetries, or permutations, of the roots of fifth-degree polynomial equations are more complex than are the symmetries that can be represented by arithmetical formulas. This fact emerged from the development of the idea of a permutation group by Galois and, independently at about the same time, by Niels Abel. Half a century later, another Norwegian, Sophus Lie, showed how important groups are to the whole of mathematics. The theory of what became known as Lie groups links the discrete structure of permutations with the continuous variation of differential equations. Not surprisingly, because group theory forms a common underpinning to algebra and to geometric features such as rotation, reflection, and symmetry, it crops up routinely in modern physics, from the classification of elementary particles to crystallography.
Types of groups
Groups come in two main types – finite and infinite. The symmetry group of the roots of a polynomial equation is a finite group, because there is only a limited number of permutations possible among the roots of a given polynomial. In contrast, the Lie groups that represent symmetries of solutions of differential equations are infinite because they represent continuous transformations, and continuity carries the potential of an infinite number of changes.
Finite groups can be built up from combinations of smaller groups by a process analogous to multiplication. In the same way that a whole number can be written as a product of prime numbers, a finite group can be expressed as a combination of certain factors known as simple groups. Most simple groups belong to one of three families: the cyclic groups, the alternating groups, or the groups of Lie type. Cyclic groups consist of cyclic permutations of a prime number of objects. Alternating groups consist of even permutations – those formed by interchanging the positions of two objects an even number of times. Sixteen subfamilies make up the simple groups of Lie type, each associated with a family of infinite Lie groups. (Confusingly, a Lie group is not a group of Lie type, since the former is infinite and the latter is finite!)
Altogether, there are 18 specific families of finite simple groups. There are also 26 simple groups, known as sporadic groups, that are highly irregular and fall outside these families. Five sporadic groups were found in the nineteenth century by Emile Mathieu. Then came a hiatus until the 1960s, when a suddenly a rush of new sporadics came to light. The most remarkable of these is the so-called Monster group, which appears to be intimately related to the structure of the universe at the subatomic level.
Fundamental group
A fundamental group is a group of a topological space X that is constructed by looking at how closed paths in X can be combined to get new paths. Under a suitable way of identifying paths (known as homotopy) one can get a group structure on the set which gives an algebraic invariant of the space X.
Simple group
A simple group is a group that has no non-trivial proper normal subgroups. Simple groups are important because they can be thought of as the blocks out of which other groups can be built. Much effort has been expended in the classification of all finite simple groups.
Semigroup
A semigroup is a set together with a method of combining elements, such as addition or multiplication, to get new ones, which satisfies only some of the properties required to get a group. In particular, a semigroup need not have an identity element and elements need not have inverses.
Subgroup
A subgroup is a subset of a group that is a group under the same operation.
Topological group
A topological group, also called a continuous group, is a set that has both the structure of a group and of a topological space in such a way that the operations defining the group structure give continuous maps in the topological structure. Many groups of matrices give topological groups.


