matrix

In mathematics, a matrix is a square or rectangular array of numbers, symbols, or mathematical expressions, usually written enclosed in a large pair of parentheses. Matrices, which are added and multiplied using a special set of rules, are extremely useful for representing quantities, particularly in some branches of physics. A matrix can be thought of as a linear operator on vectors. Matrix-vector multiplication can be used to describe geometric transformations such as scaling, rotation, reflection, and translation.

A general 3×3 matrix

The word "matrix", which literally means "womb" and is related to mater, was introduced into common English usage around 1850 by James Sylvester who demonstrated that any matrix could give rise to smaller determinants (or "minors") through the removal of some of the original's elements or entries. However, he didn't fully appreciate their potential. Within a year of his first use of the term, Sylvester introduced the idea his colleague Arthur Cayley who was the first to publish the inverse of a matrix and to treat matrices as purely abstract mathematical forms. The use of mathematical arrays to solve problems predates the application of the name by about 2,000 years. Around 200 BC in the Chinese text Juizhang Suanshu (Nine Chapters on the Mathematical Arts) the author solves a system of three equations in three unknowns by placing the coefficients on a counting board and solving by a process that today would be called Gaussian elimination. "Matrix" comes from the same Latin root that gives us 'mother', and was used to refer to the womb and to pregnant animals. It became generalized to mean any situation or substance that contributes to the origin of something.

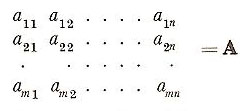A is described as an m × n matrix over F, where F is a field, without characteristic, to which all of the mn elements of A belong. A is made up of m1 × n matrices (row vectors) and nm × 1 matrices (column vectors).

The main diagonal In the square matrix [a_ij], the elements a₁₁, a₂₂, ..., a_nn, running from the top left corner to the bottom right corner.

Types of matrix

A diagonal matrix is a matrix that has 0 entries along all nondiagonal entries, i.e., only the main diagonal may have non-zero values.

A unimodular matrix is a square matrix whose determinant is 1.

A Hankel matrix is one in which all the elements are the same along any diagonal that slopes from northeast to southwest.

A Jordan matrix (or Jordan block), is one whose diagonal elements are all equal (and nonzero) and whose elements above the principal diagonal are equal to 1, but all other elements are 0.

A Toeplitz matrix is one in which all the elements are the same along any diagonal that slopes from northwest to southeast.

Addition

If two matrices A and B of F are both m × n, the result of their addition is defined to be the m × n matrix of which a typical element (a_ij + b_ij). Their addition is thus commutative and associative. Moreover, the set of m × n matrices of F forms an Abelian group under addition since it has an identity element (see group), O, the zero matrix whose elements are all zero, since A + O = A for all A, and since every A has an inverse = -A, whose typical element is (-a_ij), such that A + (–A) = O.

Multiplication

If l is an element of F, the product lA is defined as the matrix whose typical element is la_ij. Multiplication of one matrix by another is possible only if the first has the same number of columns as the second has rows. If A is an m × n and B an n × p matrix then their product AB is an m × p matrix with typical element

a_i₁b₁_j + a_i₂b₂_j + ... + a_inb_nj

Notice that, in this case, BA does not exist unless p = m since otherwise B does not have the same number of columns as A has rows.

Transposition and symmetry

The transpose of an m × n matrix A is an n × m matrix A', obtained by setting the row vectors of A as the column vectors of A', the column vectors of A as the row vectors of A'. Some basic results emerge:

    (A')' = A,
    (AB)' = B'A',
    and (kA + lB)' = kA' + lB',

where k, l, are elements of F. A matrix A is termed symmetric when A = A' and skew-symmetric when A = –A': of course, only matrices where n = m can be symmetric or skew-symmetric. For symmetry the element a_ij in A must equal a_ji for all i, j; for skew-symmetry a_ij + a_ji = 0, for all i, j. See also determinant.