vector
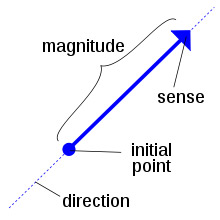
A vector is a quantity that has both magnitude and direction, unlike a scalar, which has only magnitude. Examples of vectors include velocity, acceleration, and force. The velocity of an object is specified by its speed and its direction in which it is moving at any instant. Similarly, a force has both magnitude and direction, hence weight (the force of gravity on a body) is a vector. In contrast, mass and temperature are scalar quantities.
In three-dimensional space, a vector is represented by a list of three numbers. Geometrically, these three values specify an arrow with direction and magnitude.
Vectors are added when, for instance, movement takes place in a frame of reference that is itself moving (for example, as when a swimmer tries to cross a flowing river). Vectors are added like arrows, end to end, so that in the case of two vectors, the sum is the vector from the tail of the first to the tip of the second. Vectors are a specific type of tensor.
Terms related to vectors
curl
The curl of a vector is the vector product of del with the vector. Thus (in Cartesian coordinates):
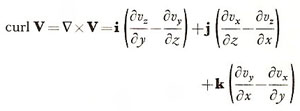
del
Del, also known as alted or nabla, is the vector operator Δ, expressed in Cartesian coordinates as
![]()
The product of Δ and a scalar S yields a vector field called grad S (the gradient of S):
![]()
The scalar product of Δ with a vector V is the divergence of V (div); the vector product of Δ with V is the curl of V.
div
In vector analysis, div is divergence. Div V is defined as the scalar product of del with the vector V: ΔV. Hence in Cartesian coordinates,
![]()
position vector
A vector whose point of origin is the origin of a coordinate system, and whose end-point is some other point. Position vectors cannot, like other vectors, be freely moved parallel to themselves; they are bound to the origin of the coordinate system.
vector field
A set of vectors such that every point in a particular region of space R is associated with a single vector. A familiar example of a vector field in nature is a magnetic field.


