vector analysis
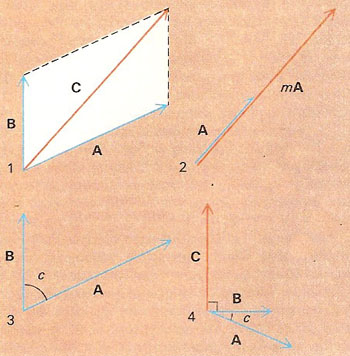
Vector algebra. (1) Addition of vectors A and B yields vector C according to the parallelogram rule. (2) Multiplication of vector A by scalar m yields vector mA. (3) The scalar product of vectors A and B, A.B = AB cos c. (4) The vector product of vectors A and B, A × B = C, where C = (AB cos C)n and n is a unit vector perpendicular to the plane containing A and B.
Vector analysis is the application of the techniques of analysis and algebra to the study of vectors. Since vector quantities have both magnitude and direction, they may be represented geometrically by lines with specified directions, whose lengths represent the magnitudes of the vectors concerned; the magnitude of a vector V is written V.
The dot (or scalar) product of two vectors A and B inclined at angle c to each other is defined as A.B = AB cos c. The cross (or vector) product of two vectors A and B inclined at an angle c to each other is defined as A × B = (AB sin c)n where n is a unit vector whose direction is perpendicular to the plane of A and B such that, looking along the direction of n, a clockwise turn of less than 180° is required to bring A into B. See also complex number.


