complex number
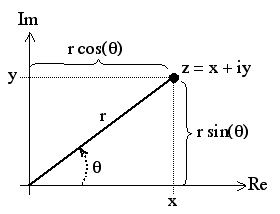
Figure 1. A complex number represented on the Argand diagram.
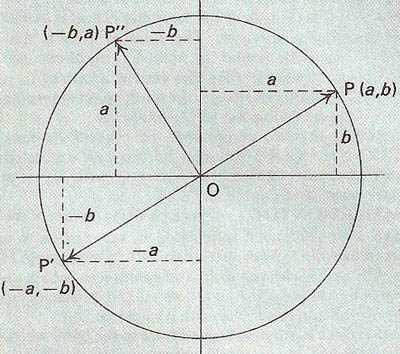
Figure 2. The imaginary operator i rotates the vector OP into OP", and – on a second application – rotates OP" into OP'.
A complex number is a real number plus a real number times the square root of –1; in other words, a number of the form z = a + ib, where a and b are real and i = √(–1). The term ib is known as an imaginary number or the imaginary part of the complex number a + ib; a is called the real part. The names "complex," "real," and "imaginary," which came about historically, are totally misleading because complex numbers are not particularly complex and imaginary numbers are no less real than real numbers! Another way to represent a complex number is as an ordered pair of real numbers (a, b) together with the operations: (a, b) + (c, d) = (a + c, b + d) and (a, b) × (c, d) = (ac – bd, bc + ad). Alternatively, complex numbers can be shown as points on an Argand diagram (a representation of the complex plane) in which the horizontal axis is the real number line and the vertical axis represents all possible purely imaginary numbers. Any point that appears on the complex plane off-axis has both real and imaginary parts. On an Argand diagram a complex number can also be shown as a vector, or directed line segment (a line of a certain length with an arrow), extending from the origin (0 + 0i) to the number (a + bi). The absolute value or magnitude of a complex number z, thought of as a point on a plane, is its Euclidean distance from the origin, and is denoted |z|; this is always a non-negative real number. Algebraically, if z = a + ib, we can define |z| = √(a2 + b2). If the complex number z is written in polar coordinates z = r eiφ, then |z| = r.
Complex numbers are a natural extension of the real numbers and form what is called an algebraically closed field. Because of this, mathematicians sometimes consider the complex numbers to be more "natural" than the real numbers: all polynomial equations have solutions among the complex numbers, which is not true for the real numbers. Complex numbers are used in electrical engineering and other branches of physics as a convenient description for periodically varying signals. In an expression z = r eiφ one may think of r as the amplitude and phi as the phase of a sine wave of given frequency. In special and general relativity theory, some formulas for the metric on spacetime become simpler if the time variable is taken to be imaginary.
Imaginary number
An imaginary number is a number whose square is negative. Every imaginary number can be written in the form ib where b is a real number and i is the imaginary unit, √–1, with the property that i 2 = –1. For example, √–16 is an imaginary number, since √–16 = √–1.√16 can be written as 4i.
Imaginary numbers are complex numbers in which the real part is zero. In the representation of complex numbers on the complex plane (Argand diagram), imaginary numbers lie on the y-axis.
The "imaginary" in the term is a vestige from the time when mathematicians had not yet defined a number system to accommodate numbers whose square is less than or equal to zero. Greek mathematician and engineer Hero of Alexandria (c. 10–70 AD) is credited with the concept of imaginary numbers, but it was Rafael Bombelli who first codified and thoroughly described their properties in his treatise L'Algebra (1572). He defined an imaginary number a the square root of minus one and gave it the symbol i.
Imaginary operator
An imaginary operator, also called an i-operator or joperator, is the part of a complex number that defines the magnitude of the part of the complex number at right angles to the real number part. It may be understood as follows: consider a vector OP where O is the origin of a set of Cartesian coordinates and P is the point (a, b) – see diagram. Multiplying OP by -1 will produce a vector OP'; that is, it will rotate OP through 180° such that OP' = –OP. Now consider a number i (called the imaginary operator) such that multiplying OP by i produces OP", a vector perpendicular to OP. Multiplying OP" by i will produce OP'.
Argand diagram
An Argand diagram, also known as the Argand plane or the complex plane, is a way of representing complex numbers as points on a coordinate plane using the x-axis as the real axis and the y-axis as the imaginary axis. It is named for the French amateur mathematician Jean Robert Argand (1768–1822) who described it in a paper in 1806.1 A similar method had been suggested 120 years earlier by John Wallis and had been developed extensively by Casper Wessel. But Wessel's paper was published in Danish and wasn't circulated in the languages more common to mathematics at that time. In fact, it wasn't until 1895 that his paper came to the attention of the mathematical community – long after the name "Argand diagram" had stuck.
In Figure 1, a complex number z is shown in terms of both Cartesian (x, y) and polar (r, θ) coordinates.
Reference
1. Argand, R. Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques. Paris: Albert Blanchard, 1971. Reprint of the 2nd ed., published by G. J. Hoel in 1874. First edition published Paris, 1806.

