differential equation
A differential equation is a description of how something continuously changes over time. Differential equations occur in many, if not most, physical problems. Some differential equations have an exact analytical solution such that all future states can be known without simulating the time evolution of the system. However, most have a numerical solution with only limited accuracy.
A differential equation involves the first or higher derivatives of the function to be solved for. If the equation only involves first derivatives it is known as an equation of order one, and so on. If only n-th powers of the derivatives are involved, the equation is said to have degree n. Equations of degree one are called linear. Equations in only one variable are called ordinary differential equations to distinguish them from partial differential equations, which have two or more.
Example of a differential equation and its solution
Consider an object accelerating (see acceleration) uniformly at 40 meters per second per second. After a time t it has a velocity 40t, assuming a stationary start. This velocity may be expressed as ds/dt, the instantaneous rate of change of distance, s. Thus
40t = ds/dt
To find out the distance traveled by the object after a time t we can integrate to find
20t 2 + k = s + c
or s = 20t 2 + (k – c)
where k and c are constants. However, we have assumed a stationary start, i.e., that when t = 0, s = 0 and hence, by substitution, (k – c) = 0. Therefore, to find out how far the body has traveled after a given period of time, we need merely to substitute the value of t into
s = 20t 2
This is the solution of a very simple first-order differential equation.
Higher order differential equations
In some problems there occur second derivatives of the form d 2y/dx2, and these involve solutions of second-order differential equations. Equations involving nth derivatives, d ny/dxn, are called nth-order equations, most important of which are equations of the form
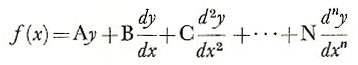
where A, B, C, ..., N are constants. This is termed a linear nth-order differential equation.


