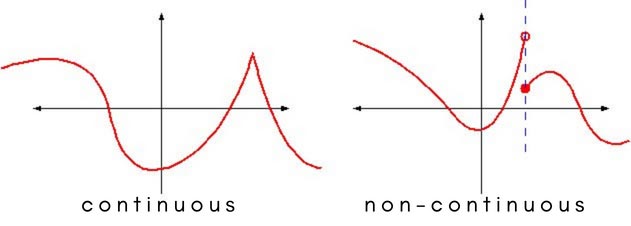
Continuity is a mathematical property that has to do with how smooth or "well-behaved" a function or curve is. If two adjacent points on a graph, for example, are not connected or are separated by a jump, this marks a breakdown of continuity. At such a discontinuity it is impossible to obtain a derivative, or slope, of the curve. Usually if a curve does misbehave like this, it is only at one or two isolated places; elsewhere the curve is likely to be both continuous and differentiable.

 

However, it is possible to construct a continuous function that has "problem points" everywhere and, therefore, is nowhere differentiable! The first example was found by Karl Weierstrass in 1872 and came as a total surprise. It is defined as an infinite series:

 

 

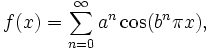
where a and b can be any numbers such that a is between 0 and 1, and a × b is bigger than 1 + (3π/2).