derivative
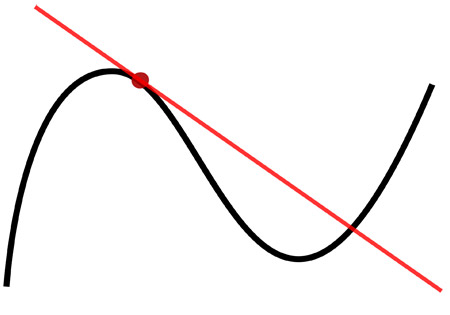
A function (black) and a tangent (red). The derivative at the point is the slope of the tangent.
A derivative is the result of differentiating a function; that is, the infinitesimal change in a function caused by an infinitesimal change in the variable(s) upon which it depends. The derivative gives the rate of change of a function (the slope of its curve) at a particular point. Second and third derivatives give the rate at which the rate of change is changing and the rate at which the rate of rate of change is changing, respectively.
The derivative of a function f(x), at the point x, is defined to be the value of the ratio
[f(x + h) - f(x)]/h,
In the limit where the number h approaches zero, and is denoted df /dx or f '(x).
Derivatives provide a means of describing many processes which can be viewed as changing continuously in time. For instance, if the position of an object at a time, t, is given by p(t) then the velocity (which is defined as the instantaneous rate of change of position), obtained by differentiation, is given by the derivative dp/dt.
In an article in 1996, Hugo Rossi wrote: "In the fall of 1972 President Nixon announced that the rate of increase of inflation was decreasing. This was the first time a sitting president used the third derivative to advance his case for reelection."1
Partial derivative
The partial derivative is the ordinary derivative of a function of two or more variables with respect to one of the variables, the others being considered constants. If the variables are x and y, the partial derivatives of f(x, y) are written δf/δx and δf/δy, or Dxf and Dyf, or fx and fy. The partial derivative of a variable with respect to time is known as the local derivative.
Reference
1. Rossi. Hugo. "Mathematics Is an Edifice, Not a Toolbox." Notices of the AMS, 43 (10) (Oct. 1996).


