symmetry

The symmetry of a snowflake echoes the symmetry of its molecules but owes its elaborate perfection to the subtle process of crystal growth by vapor-deposition on a vibrating surface.
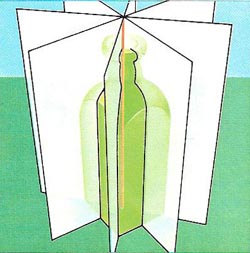
If a square-shaped bottle is rotated through 90 degrees about its vertical axis, it presents its original appearance again. The axis is thus a fourfold axis of rotational symmetry. The bottle's other symmetry elements are four mirror planes.

A bottle with a blank label has no rotation axis and only one mirror plane as symmetry element.

This pseudo-bottle has new symmetry elements: a horizontal mirror plane H and four twofoldaxes in it, as well as a center of inversion I, about which the bottle can be rotated and remain unchanged.
Symmetry is an intrinsic property of a mathematical object that allows it to remain unchanged under certain types of transformation, such as rotation, reflection, or more abstract operations. The mathematical study of symmetry is systematized and formalized in the extremely powerful subject known as group theory. Symmetries and apparent symmetries in the laws of nature have played a part in the construction of physical theories since the time of Galileo and Newton. The most familiar symmetries are spatial or geometric ones. In a snowflake, for example, the presence of a symmetrical pattern can be detected at a glance.
Introduction
Symmetry is a powerful concept and its workings can be seen in many aspects of the world. The two halves of a bridge span, the wings of a bird or of an aircraft, the blades of a propeller, all have symmetry. Mathematicians recognize many different types of symmetry all described by the group of real or imaginable symmetry operations which leave the symmetrical entity apparently unchanged. A square, a cube, or a four-bladed propeller can all be turned through 90° without apparent change: they are said to have a fourfold axis of symmetry. An irregular object has the lowest symmetry because any twist or turn is detectable. A sphere has the highest possible symmetry; no twist or turn is detectable. This made it a figure of perfection to the ancient Greeks and makes it highly useful today. A ballrace is so simple because the balls need no aligning; no matter how they roll they cannot jam the bearing. A roller-bearing of lower symmetry needs guides to keep rollers parallel to the bearing axis; a tapered roller-bearing of lower symmetry has even more geometrical constraints.
Symmetry of nature
A snowflake shows how the laws of nature give symmetry to their products. It has 120-degree angles between many faces because in the water molecules of which is it composed two hydrogen atoms form a 120-degree angle with an oxygen atom. The crystal lattice in ice is formed by the regular interpacking of the molecules and reflects this symmetry.
But this does not explain why the whole elaborate structure has a sixfold axis of symmetry. How does one branch of the flake know how its fellows are growing, so as to imitate them exactly? The physicist Samuel Tolansky (1907–1973) made the suggestion that a snowflake, as it falls and takes up water vapor from the cold air, is vibrating with the symmetry of its crystal structure. All the branches move and twist together in a complex and changing pattern; the fastest points on each branch intercept the most water vapor and so grow together.
Such symmetries of process are common throughout nature. The radial shatter-pattern of a broken window betrays the symmetrical stresses that radiated outwards from the impact point.
Symmetry in the abstract
Mathematics manages symmetry by group theory, a fascinating topic which, from a few apparently trivial axioms, develops rapidly into a structure of amazing subtlety and elegance. The oddest thing about it is that, unlike number theory, it allows a × b not to equal b × a. This lack of symmetry in the mathematics of symmetry may seem like complete nonsense, but in practice the order of events can also be important. Sanding down a door, then painting it, for example, gives a different result from painting it and then sanding it down.
For an object with symmetry its group consists of the operations that can be carried out on it: turning it through 90 degrees, reflecting it in a plane, and so on. Take a square square-shouldered pill bottle without its label, hold it upright and pivot it through a right-angle about its top-left and bottom-right corners. It will then be horizontal with the neck on the left. Turn it clockwise through 90 degrees and it will be upright again. That is a symmetry operation. But if the latter is performed first and then the former the bottle will finish upside down: a × b does not equal b × a.
Uses of group theory
Group theory is one of the many inventions of 19th-century mathematics that later found scientific use. Indeed, the rapid spread of its strange but potent arithmetic in 20th-century physics earned it the title, among an older generation of physicists, of die Gruppenpest ("group nuisance"). But its incorporation into modern physics and chemistry, with their need to understand the subtle symmetries of molecules and crystals and their energy states has made possible the theories which give us such modern marvels as semiconductor electronics.
So much symmetry exists in scientific theories and mathematics that researchers acquire a feeling for it and any "lopsided" features of a theory or experiment make them uneasy. In electromagnetism, for instance, the fact that electric charges (positive and negative) can be isolated, whereas magnetic poles (north and south) cannot, seems somehow to be "wrong". Physicists have sought magnetic monopoles to complete the symmetry of the situation but, so far, attempts to discover such particles have been unsuccessful. But the most daring of all such insights was that of Albert Einstein when he reasoned that the speed of light (and indeed every phenomenon of physics) must be the same for all observers, no matter how fast they themselves are traveling.
One of the most remarkable developments of the past half century has been the emergence of symmetry as a central theme of subatomic physics. This came about through a series of subtle evolutions in the concept of symmetry itself. Many researchers believe that this evolutionary process has not come to an end, and that further meaning of the concept of symmetry, with perhaps new mathematical structures, will develop in the coming years.
Reference
1. Weyl, Hermann. Symmetry. Princeton, NJ: Princeton University Press, 1952.


