sphere

Figure 1. A mathematical surface can be defined like a curve, using three mutually perpendicular axes in space, x, y, z. The equation of a sphere with its center at the origin is x 2 + y 2 + z 2 = r 2. All points outside it have x 2 + y 2 + z 2 greater than r 2; those inside have x 2 + y 2 + z 2 less than r 2; the equation balances on the boundary. An equation such as x 2 + y 2 + z 2 = r 2– 2x – 8z + 17 also defines a sphere but its center is not at the intersection of the three axes.

Figure 2. Abell 39. Credit: George Jacoby (WIYN Obs.) et al., WIYN, AURA, NOAO, NSF.
A sphere is a surface made from all the points that are an equal distance from a given central point. Sometimes an actual sphere, which is two-dimensional, may be confused with the three-dimensional object that includes all the points inside this surface. However, mathematicians make a sharp distinction and call the latter a ball.
 |
A sphere is a two-dimensional object that can be embedded in three-dimensional space. A quadric, it is the set of all points in three-dimensional Euclidean space that lie at distance r, the radius, from a fixed point. In coordinate geometry a sphere with center (x0, y0, z0) and radius r is the set of all points (x, y, z) such that
(x – x0)2 + (y – y0)2 + (z – z0)2 = r 2
A sphere can also be defined as the surface of revolution formed by rotating a circle about its diameter. If the circle is replaced by an ellipse, the shape becomes a spheroid.
The surface area of a sphere is 4πr 2 and its volume is 4πr 3/3. The sphere has the smallest surface area among all surfaces enclosing a given volume and it encloses the largest volume among all closed surfaces with a given surface area. In nature, bubbles and water drops tend to form spheres because surface tension always tries to minimize surface area.
A zone is the area of a that part of a sphere lying between two given parallel planes.
The intersection of a sphere and any plane is circular; should the plane pass through the center, the intersection is a great circle.
The circumscribed cylinder (see circumscription) for a given sphere has a volume which is 3/2 times the volume of the sphere. If a spherical egg were cut up by an egg-slicer with evenly spaced wires, the bands between the cuts (on the surface of the sphere) would have exactly the same area.
Spheres can be generalized to other dimensions. For any natural number n, an n-sphere is the set of points in (n + 1)-dimensional Euclidean space that lie at distance r from a fixed point of that space. A 2-sphere is therefore an ordinary sphere, while a 1-sphere is a circle and a 0-sphere is a pair of points. An n-sphere for which n = 3 or more is often called a hypersphere.
Dandelin spheres
If a cone is sliced through by a plane, the two spheres that just fit inside the cone, one on each side of the plane and both tangent to it and touching the cone, are known as Dandelin spheres. They are named after the Belgian mathematician and military engineer Germinal Pierre Dandelin (1794–1847) who gave an elegant proof that the two spheres touch the conic section at its foci. In 1826, Dandelin showed that the same result applies to the plane sections of a hyperboloid of revolution.
 |
| Dandelin spheres. Image by Hop David, used with permission.
|
Dupin cyclide
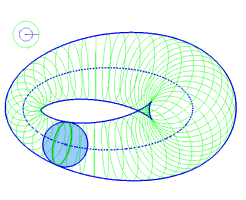
|
| Image credit: Robert March.
|
A Dupin cyclide is the envelope of all spheres touching three given fixed spheres. (Each of the fixed spheres is to be touched in an assigned manner, either externally or internally.) Equivalently, it is the envelope of all spheres whose centers lie on a given conic section and which touch a given sphere. Also equivalently, it is the inverse of a torus.
Spheres in space
Abell 39 (Figure 2) is an almost perfectly spherical planetary nebula in the constellation Hercules. Discovered in 1966 by George Abell, it is one of the largest known spheres in our Galaxy. Its shape has allowed astronomers to accurately estimate how much relative material in the nebula is absorbing and emitting light. Observations indicate that Abell 39 has only about half the abundance of oxygen found in the Sun. The reason why the central star is slightly off center, by 0.1 light-year, is currently unknown.
| visual magnitude | 13.7 (integrated); 15.7 (central star) |
| angular diameter | 3.9' |
| linear diameter | 5 light-years |
| distance | ~ 7,000 light-years |
| position | RA 16h 27m 32.6s; Dec +27° 54' 29" |
| other designations | PNG 047.0+42.4, PK 047+42.1, ARO 180 |


