spherometer
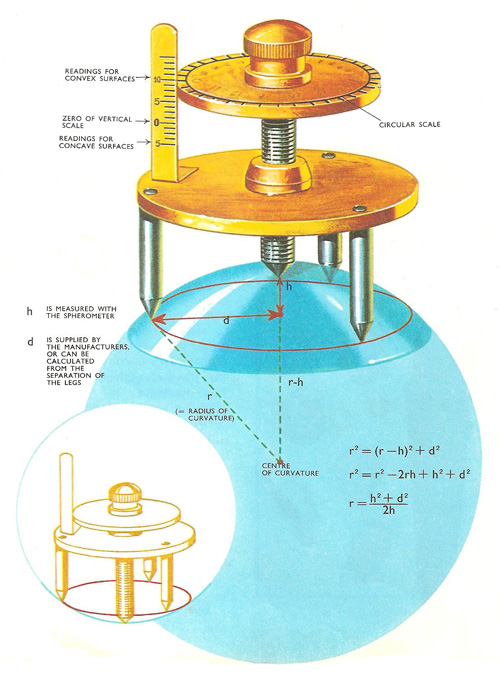
The spherometer is used to find the radius of curvature of spherical surfaces. Large picture: a convex surface. Insert: a concave surface.
A spherometer is an instrument used for measuring the radius of curvature of a spherical surface. Spherometers were first used by opticians to measure the curvature of the surface of a lens.
Anton von Leeuwenhoek, the Dutch microscopist who specialized in setting and grinding lenses, used a small, almost spherical glass lens in his simple microscope. With this lens he was able to examine the structure of skin, and discover bacteria. One single lens was able to give quite a high magnification because it was small and almost spherical. The image-forming properties of all lenses (and mirrors) depend on the curvature of their surfaces – whether they are sharply curved as in Leeuwenhoek's small spheres or shallower curves which are part of much larger spheres. Lens and mirror surfaces are usually parts of spheres.
It isn't the radius of the lens or mirror itself which is of primary importance, but the radius of the sphere to which the curved surface of the lens belongs. This radius is called the radius of curvature, and is the quantity measured by a spherometer.
The spherometer has three straight legs all of the same length that are at the same level and arranged so that their tips form an equilateral triangle. A fourth leg is of adjustable length, and its tip is at the center of the triangle. The spherometer is placed on the lens or mirror surface. Since its outer legs are over an inch (2.5 cm) apart, and all legs must touch the surface, the spherometer cannot be used on very small lenses or mirrors.
The central leg is adjusted so that all four tips touch the surface at the same time. If the surface is concave (rounded like the bowl of a spoon), the central leg must be longer for the spherometer to fit the surface. On a convex surface (rounded like the back of a spoon), the central leg must be shorter. This central leg is screwed up and down, and a circular disk with a scale marked around its outer edge is fixed to the head of the screw. The disk moves up and down a fixed vertical scale. Both scales are used to measure the difference in height between the fixed legs and the adjustable leg. The vertical scale shows an approximate value of the height difference. Each of its scale divisions corresponds to one complete twist of the screw. The circular scale is marked in fractions of complete screw turns. It gives the additional fraction of a twist (between the vertical scale markings) accurately.
The height difference is directly related to the radius of curvature, which can be calculated from the height difference by a simple formula. A shallow curve gives a small difference in level, and a large radius of curvature. Obviously a shallow lens is a small part of a large sphere. A more sharply curved surface gives a bigger height difference and a smaller radius of curvature.
Before the spherometer is used, its zero reading must be checked for accuracy. A flat surface gives a zero height difference and the spherometer is supplied with a piece of flat plate glass on which the instrument can be checked. The vertical scale zero is not at either end of the scale, but somewhere near the middle of it. This is so that both positive and negative height differences, corresponding to convex and concave surfaces, can be measured with the spherometer.


