PLANE CURVES

Figure 1. Caustic curves appearing as reflections of light in the surface of water.
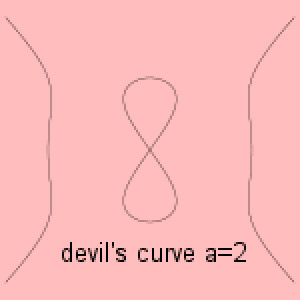
Figure 2. The Devil's curve. Image: Jan Wassenaar www.2dcurves.com.
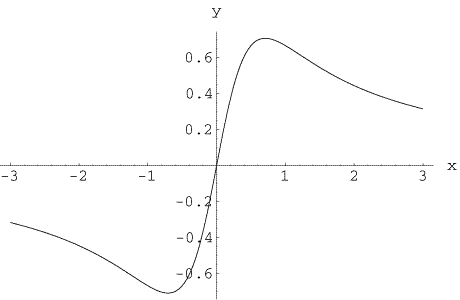
Figure 3. A Serpentine curve.

Figure 4. Unduloid droplets on a spider's web.
anallagmatic
curve
arbelos
arc
Archimedean
spiral
astroid
asymptote
bicorn
bicuspid curve
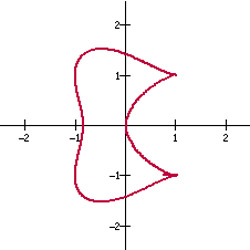 |
A bicuspid curve is a quartic curve given by the equation
(x 2 – a 2)(x – a)2 + (y 2 – a 2)2 = 0.
Bowditch curve
brachistochrone
caduceus
cardioid
 |
A cardioid is a heart-shaped curve first studied in 1674 by the Danish astronomer Ole Römer who was trying to find the best shape for gear teeth. The curve appears to have been named by Giovanni Salvemini de Castillon (1708–1791).
When a circle rolls around another circle of the same size, any point on the moving circle traces out a cardioid. The Greeks used this fact when attempting to describe the motions of the planets. The cardioid is also the envelope of all circles with centers on a fixed circle, passing through one point on the fixed circle. In polar coordinates, it has the equation
r = 2a (1 – cos θ).
It can also be described as an epicycloid with one cusp.
Cartesian oval
Cassinian ovals
catenary
caustic curve
A caustic curve is the envelope of rays of light reflected (or refracted) by a given curve from a given point source of light. A catacaustic results from reflection (Figure 1), a diacaustic from refraction.
Among the caustic curves of a circle are limaçon, if the light source is nearby, a nephroid, if the source if at infinity, and a cardioid, if the source is on the circle.
Cayley's sextic
chord
circle
circle involute
circumcircle
cissoid
closed curve
cochleoid
A cochleoid is a spiral curve that was first studied by J. Peck in 1700 and Bernoulli in 1726. Its name, meaning "snail-form" (kochlias is Greek for "snail"), was coined by Benthan and Falkenburg in 1884.
The cochleoid can be constructed as follows: given a point O and the y-axis. For all circles through O (hence tangent to the y-axis), place a constant distance on the circle. The collection of these points is the cochleoid. In Cartesian coordinates, it is given by the formula
(x 2 + y 2) tan–1(y /x) = ay
and in polar coordinates by
r = a sinθ / θ
The points of contact of parallel tangents to the cochleoid lie on a strophoid.
conchoid
conic section
crunode
cubic curve
A cubic curve is an algebraic curve described by a polynomial equation of the general form:
ax 3 + bx 2y + cxy 2 + dy 3 + ex 2 + fxy + gy 2 + hx + iy + j = 0,
where a, b, c, d, e, f, g, h, i, and j are constants, such that at least one of a, b, c, and d is non-zero, and x and y are variables.
One of Isaac Newton's many accomplishments was the classification of the cubic curves. Newton found 72 different species of curve. Later investigators found six more, and it is now known that there are precisely 78 different types of cubic curves. Interesting examples include the folium of Decartes and the Witch of Agnesi (see Agnesi, Maria).
curve of constant width
cusp
In mathematics, a cusp is a point on a curve where two branches, coming from different directions, meet and have a common tangent. If the two branches of the curve approach the tangent from opposite sides the cusp is called a keratoid (from the Greek kera for horn) or first-order cusp. This is the case, for example, with the curve given by the equation y 2 = x 2y + x 5. If the two branches of the curve approach the tangent from the same side the result is a ramphoid or second-order cusp. The curvature at a cusp is infinite.
"Cusp" derives from the Latin cuspis for sharp. Outside of mathematics, the points of a crescent moon are called cusps and the sharp pointed premolar teeth of children are known as bicuspids. See Reuleaux triangle and rotor.
cycloid
de l'Hopital's cubic
delta curve
The delta curve is a curve that can be turned inside an equilateral triangle while continuously making contact with all three sides. There are an infinite number of delta curves, but the simplest are the circle and lens-shaped delta-biangle. All the delta curves of height h have the same perimeter, 2πh/3.
deltoid
devil's curve
The devil's curve, also known as the devil on two sticks, is a curve with the Cartesian equation
y 4 -– a 2y 2 = x 4 – b 2x 2
and the polar equation
r 2(sin2θ - cos2θ) = a 2sin2θ – b 2cos2θ.
Early studies of it were carried out in 1750 by the Swiss mathematician
Gabriel Cramer (1704–1752), who is most famous for his work on determinants,
and in 1810 by Lacroix. For a = 25/24, the curve is called the
directrix
Dürer's shell curve
egg
eight curve
The eight curve is a curve, also known as the lemniscate of Gerono, that has the Cartesian equation
x 4 = a 2 (x 2 – y 2)
and the appearance of a figure eight lying on its side (like the symbol for infinity).
ellipse
epicycloid
epitrochoid
An epitrochoid is a curve traced out by a point that is a distance c from the center of a circle of radius b, where c < b, that is rolling around the outside of another circle of radius a. It is described by the parametric equations
x = (a + b) cos(t ) – c cos[(a /b + 1)t ],
y = (a + b) sin(t ) - c sin[(a /b + 1)t ].
Closely related to the epitrochoid are the epicycloid, hypocycloid, and the hypotrochoid. An example of an epitrochoid appears in Albrecht Dürer's work Instruction in Measurement with Compasses and Straightedge (1525).
evolute
The evolute is the locus of the centers of curvature (the envelope) of a plane curve's normals. The original curve is then said to be the involute of its evolute. For example, the evolute of an ellipse is a Lamé curve and the evolute of a tractrix is a catenary.
Flower of Life
 |
The Flower of Life is one of the beautiful arrangements of circles found at the Temple of Osiris at Abydos, Egypt. The pattern also appears in Phoenician art from the 9th century BC. The circles are placed with six-fold symmetry, forming a mesmerizing pattern of circles and lenses. A related design from the same temple, which recurs in Italian art from the thirteenth century, is the so-called Seed of Life.
folium
Freeth's nephroid
glissette
If there are two fixed curves, and a curve S of fixed shape and length that slide with its ends on the fixed curves, then the locus of a point moving with S is called a glissette. An example is the locus of the midpoint of a line segment sliding with its ends on two perpendicular lines; this locus is a circle.
hippopede
hyperbola
hypocycloid
hypotrochoid
A hypotrochoid is a curve formed by the path of a point attached to a point c, which is not on the circumference, of circle of radius b that rolls around the inside of a larger circle of radius a. The parametric equations for a hypotrochoid can be written as:
x = (a – b) cos t + c cos(a /b – 1)t,
y = (a – b) sin t - c sin(a /b – 1)t.
The hypotrochoid is a generalized hypocycloid and comes in two varieties: a prolate hypocycloid if the starting point is outside the circumference of the rolling circle and a curtate hypocycloid if the starting point is inside the rolling circle. In the same family of curves as the hypotrochoid (and hypocycloid) are the epicycloid and epitrochoid.
involute
Attach a string to a point on a curve. Extend the string so that it is tangent to the curve at the point of attachment. Then wind the string up, always keeping it taut. The locus of points traced out by the end of the string is called the involute of the original curve, and the original curve is called the evolute of its involute.
Although a curve has a unique evolute, it has infinitely many involutes corresponding to different choices of initial point. An involute can also be thought of as any curve orthogonal to all the tangents to a given curve. See also circle involute.
isochrone
An isochrone is a set of points with the property that a given process or trajectory will take the same length of time to complete starting from any point in the isochrone. The curve formed by such a set of points is called an isochronous curve. See also tautochrone problem
kampyle of Eudoxus
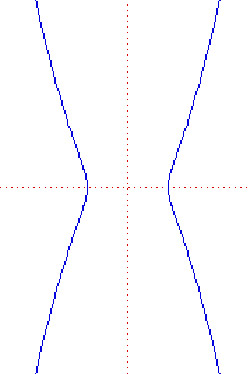 |
The kampyle of Eudoxus is an hour-glass-shaped curve that was first studied by Eudoxus in an attempt to solve the classical problem of duplicating the cube. It is described by the Cartesian equation
a 2x 4 = b 4(x 2 + y 2)
It is also the radial curve of the catenary.
kappa curve
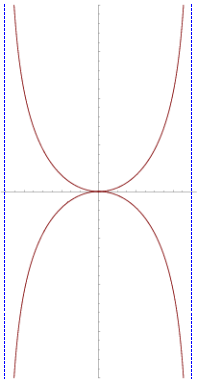 |
The kappa curve, also known as Gutschoven's curve after Gérard van Gutschoven (1615–1668) who first studied it around 1662, resembles the Greek letter kappa (κ), It was also investigated by Isaac Newton and, some years later, by Johann Bernoulli. The kappa curve is given by the Cartesian equation:
y 2(x 2 + y 2) = a 2x 2
Lamé curve
lemniscate
limaçon of Pascal
Lissajous figure
lituus
The lituus is a spiral curve that was discovered by the English mathematician Roger Cotes (1682–1716) and named by the Scottish mathematician Colin Maclaurin in 1722. The Latin lituus refers to a staff shaped like a bishop's crosier. The lituus is the locus of a point that moves in such a manner that the area of a circular sector remains constant. The equation of the curve in polar coordinates is
r 2 = a 2/π
logarithmic spiral
Maclaurin trisectrix
Malfatti circles
Neile's parabola
nephroid
parabola
Pearls of Sluze
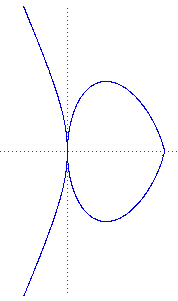 |
The Pearls of Sluze are curves that are generated by the Cartesian equation
y n = k(a – x) p x m
where n, m, and p are integers. They were first studied by the French mathematician René de Sluze (1622–1685) between 1657 and 1698 and were named the Pearls of Sluze by Blaise Pascal.
pedal curve
A pedal curve is the locus of the feet of the perpendiculars from a given point to the tangents to the given figure. The "given point" is known as the pedal point.
Plateau curves
pursuit curve
A pursuit curve is the path an object takes when chasing after another object in the most effective way. Pursuit curves can arise in a variety of situations, for example when a fox is chasing after a gazelle or a heat-seeking missile is homing in on a moving target. Suppose that four ants are at the corners of a square. They start to crawl clockwise at a constant rate, each moving toward its neighbor. At any instant, they mark the corners of a square. As the ants get closer to the original square's center, the new square they define rotates and diminishes in size. In reaching the center, each ant travels on a logarithmic spiral with a length equal to the side of the original square. Superimposed snapshots of the ants' progress add up to an intriguing pattern.
quadratrix of Hippias
 |
The quadratrix of Hippias, also called the quadratrix of Dinostratus, is the first curve in recorded history that was not part of a line or a circle, and the first curve known that is not constructible in the classical sense; in other words, it can't be drawn using a straightedge and a compass alone, but instead has to be plotted point by point.
The quadratrix can be thought of as the intersection of two lines moving with constant velocity: the first line rotates (for example, counterclockwise) while the second line moves along (say, in the direction of the positive y-axis). It has the Cartesian equation y = x cot (πx / 2a).
The quadratrix was discovered by Hippias of Elis in about 430 BC and was used by him in his work on trisecting an angle and squaring the circle. In fact, its name refers to its use in turning curvilinear space into a rectangular area.
quadrifolium
ranunculoid
 |
| Ranunculoid made from lines on a circular frame.
Image courtesy: Jos
Leys
|
A ranunculoid is an epicycloid with five cusps (n = 5), named after the buttercup genus Ranunculus.
rectangular hyperbola
Reuleaux triangle
rose curve
 |
| The quadrifolium: a special case of the rose curve
|
The rose curve is a curve that has the shape of a flower with petals. It was named rhodonea ("rose") by the Italian mathematician Guido Grandi in the 1720s. It is given by the polar equation
r = a sin(nθ).
If n is odd the rose has n petals, if n is even the rose has 2n petals, and if n = 2 the rose becomes the quadrifolium. If n is an irrational number, then there are an infinite number of petals.
rotor
A rotor is a convex figure that can be rotated inside a polygon (or polyhedron) while always touching every side (or face). The least area rotor in a square is the Reuleaux triangle. The least area rotor in an equilateral triangle is a lens with two 60° arcs of circles and radius equal to the triangle altitude. There exist nonspherical rotors for the tetrahedron, octahedron, and cube, but not for the dodecahedron and icosahedron.
roulette
A roulette is a curve traced by a fixed point on a closed convex curve as that curve rolls without slipping along a second curve.
Roulette is also a gambling game in which the players bet on which slot of a rotating disk a small ball will come to rest in. On 18 August 1913, on an unbiased roulette wheel at Monte Carlo, evens came up 26 times in a row. The probability of this occurring is 1 in 136,823,184.
salinon
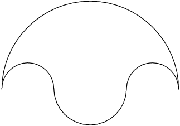 |
A salinon is a figure formed from four connected semicircles. The word salinon is Greek for "salt cellar," which the figure resembles. In his Book of Lemmas, Archimedes proved that the salinon has an area equal to the circle having the line segment joining the top and bottom points as its diameter.
serpentine
The serpentine is a curve named and studied by Isaac Newton in 1701 and contained in his classification of cubic curves (Figure 3). It had been studied earlier by de L'Hopital and Christiaan Huygens in 1692.
The curve serpentine given by the Cartesian equation
y(x) = abx/(x 2 + a 2)
shell curve
Soddy circle
 |
| Inner and outer Soddy circles (red).
|
A Soddy circle is a solution to the three-circle form of the Apollonius problem in which each of the given circles is tangent to (just touches) the other two.1 There are two Soddy circles: the outer Soddy circle, which surrounds the three given circles, and the inner Soddy circle, which is interior to them. The inner Soddy circle is the solution to the four coins problem.
Reference
1. Soddy, F. "The Kiss Precise." Nature, 137: 1021, 1936.
spiral
A spiral is a curve that turns around some central point, getting progressively closer to it or progressively farther from it, depending on which way the curve is followed. Among the best known types are the Archimedean spiral, the logarithmic spiral, the circle involute, and the lituus. Like their space-curve cousin the helix, all spirals are asymmetric and each comes in two forms that are mirror reflections of one another.
strophoid
superellipse
tautochrone
tetracuspid
tractrix
trefoil curve
A trefoil curve is a plane curve given by the equation
x 4 + x 2y 2 + y 4 = x(x 2 – y 2)
tricuspoid
trident of Newton
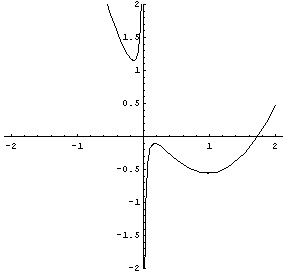 |
The trident of Newton is a curve investigated and named 'trident' by Isaac Newton as part of his systematic study of cubic equations. René Descartes also studied it and it is sometimes called the parabola of Descartes, although it isn't a parabola. It has the Cartesian equation
xy = cx 3 + dx 2 + ex + f
trifolium
trigonometric curve
trisectrix
A trisectrix is any curve that can be used in trisecting an angle. The name 'trisectrix', on its own, is often applied specifically to the limaçon of Pascal. Other famous trisectrix curves include the Maclaurin trisectrix and the conchoid of Nicomedes.
trochoid
A trochoid is the curve formed by the path of a point on the extension of a radius of a circle as it rolls along a curve or line. It is also the curve formed by the path of a point on a perpendicular to a straight line as the straight line rolls along the convex side of a base curve. By the first definition the trochoid is derived from the cycloid; by the second definition it is derived from the involute. See also roulette.
Tschirnhaus's cubic
Tschirnhaus's cubic is a curve with the Cartesian equation 3ay 2 = x(x – a) 2.
twisted cubic
A twisted cubic is a curve in three-dimensional space or projective space whose points are given by (x(t ), y(t ), z(t )) for a parameter t and where x, y, z are polynomials of degree at most 3.
unduloid
An unduloid is a member of a family curves that is formed by films or liquid drops suspended between certain boundaries. Examples of unduloids are seen on a spider web when viewed through a microscope (Figure 4). They consist of blobs of viscous liquid, which make up the sticky part of the web and are mostly gathered into a lemon shape.
The family of unduloids includes shapes ranging from very thin to almost spherical, depending on the diameter of the thread and the volume of liquid in the blob. The shape of the curve is a result of the equality of pressure throughout the blob, which means that the total curvature at all points on the surface must be the same. The total curvature is the sum as the curvatures in two planes at right angles, and so varies from one blob to the next. A common property of all unduloids, however, is that they have a constant non-zero mean curvature.
vesica piscis
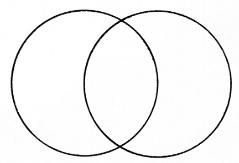 |
The vesica piscis, literally "fish's bladder," is the almond shape formed when two identical circles overlap so that the outside edge of each just touches the center of the other. The vesica piscis appears as the Christian fish symbol and also frequently in medieval art and architecture. Most significantly, it provides the template for the pointed Gothic arch.
witch of Agnesi


