epicycloid
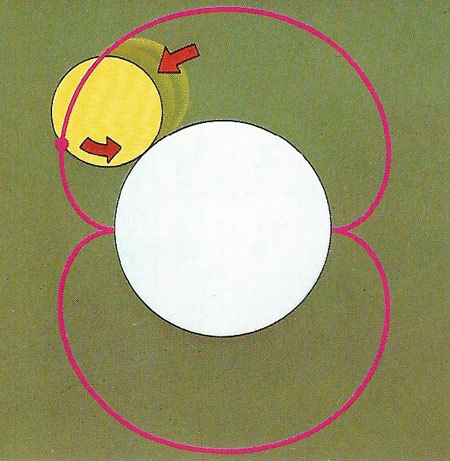
A wheel rolling on another wheel generates an epicycloid. To mesh smoothly without "stepping" from tooth to tooth, gear wheels need teeth of defined curves. The rise of an epicycloid from the inner wheel is one ideal curve. The point on the rim of a wheel rolling inside another wheel generates a curve called a hypocycloid, also used in gears.
Epicycloid is the path traced out by a point on the circumference of a circle of radius b rolling on the outside of a circle of radius a. It is described by the parametric equations:
x = (a + b) cos (t ) – b cos [(a/b + 1)t ],
y = (a + b) sin (t ) – b sin [(a/b + 1)t ].
An epicycloid is like a cycloid on the circumference of a circle and is closely related to the epitrochoid, hypocycloid, and hypotrochoid.
An epicycloid with one cusp is called a cardioid, one with two cusps is called a nephroid, and one with five cusps is called a ranunculoid (after the buttercup genus Ranunculus).


