hypocycloid
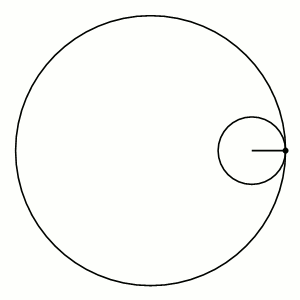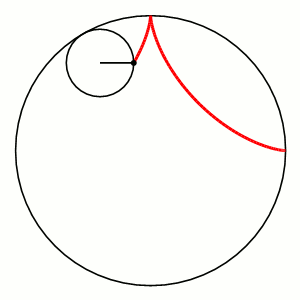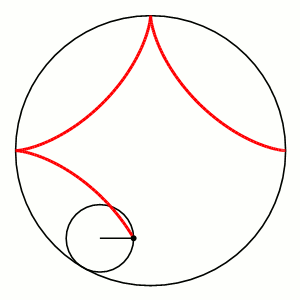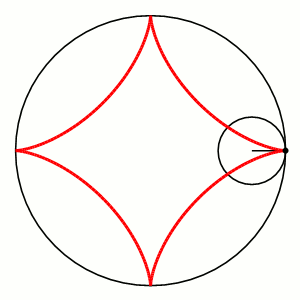
The red path is a hypocycloid traced as the smaller black circle rolls around inside the larger black circle.
A hypocycloid is a curve formed by the path of a point attached to a circle of radius b that rolls around the inside of a larger circle of radius a. The parametric equations for a hypocycloid can be written as:
x = (a – b) cos t + b cos
(a/b – 1)t,
y = (a – b) sin t – b sin (a/b – 1)t.
The type of hypocycloid depends on where the point whose path is being traced is located on the rolling circle. If it lies on the circumference of the circle, the curve generated is an ordinary hypocycloid. If it lies elsewhere the result is a hypotrochoid. A hypocycloid has a closed form – that is, the moving point eventually retraces its steps – when the ratio of the rolling circle and the larger, fixed is equal to a rational number. When this ratio is in its simplest form, the numerator is the number of revolutions covered inside the fixed circle before the curve closes. In the same family of curves as the hypocycloid (and hypotrohoid) are the epicycloid and epitrochoid.


