cycloid
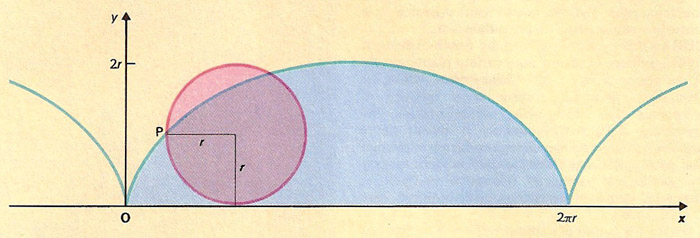
The cycloid (blue) and its generating circle (red).
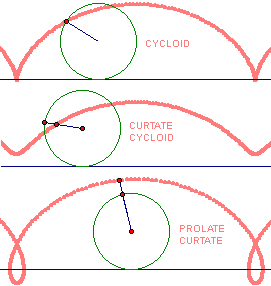
Types of cycloid.

Brachistochrone problem.

Tautotochrone problem.
A cycloid is the shape defined by a fixed point on a wheel as it rolls. More precisely, it is the locus of a point on the rim of a circle rolling along a perfectly straight line. The curve resembles a succession of arches, with cusps separated by distances equal to the circumference of the circle.
The cycloid was named by Galileo in 1599. It is the solution to both the brachistochrone problem and the tautochrone problem. In 1634, the French mathematician Gilles de Roberval (1610–1675) showed that the area under a cycloid is three times the area of its generating circle. In 1658, the English architect Christopher Wren showed that the length of a cycloid is four times the diameter of its generating circle. But there was a lot of bickering and a lack of public sharing of information around this time that led to much duplication of effort, particularly over questions related to the cycloid. In fact the confusion was so bad that the curve was nicknamed the Helen of Geometers, and Jean Montucla referred to it as "la pomme de discorde." The cycloid is of architectural interest since it forms the strongest known arch.
As well as the ordinary cycloid there is the curtate cycloid, which is the path traced out by a point on the inside of a rolling circle, and the prolate cycloid, which is followed by a point on the outside of the circle. A prolate cycloid is traced out, for example, by points on the flange of the wheels of a locomotive, which extends below the top of the tracks. This leads to the surprising conclusion that even as the locomotive is moving forward there are always parts of its wheels that are going backward for a moment before moving forward again.
Brachistochrone problem
The brachistochrone problem is a problem with which Johann Bernouilli challenged his contemporaries in Acta Eruditorum in June 1696:
Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise... Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time.
Isaac Newton reportedly solved the problem between four in the evening and four in the morning after a hard day at the Royal Mint, later commenting: "I do not love to be dunned [pestered] and teased by foreigners about mathematical things..." Other correct solutions came in from Gottfried Leibniz, the Frenchman Guillaume de L'Hôpital, and Johann's brother Jakob. They, like Johann, realized that the solution to the brachistochrone problem, as it was also to the tautochrone problem, was the cycloid. See also calculus of variations.
Tautochrone problem
The tautochrone problem is to find the curve down which an object can slide from any point to the bottom (accelerated by gravity and ignoring friction), always in the same length of time. "Tautochrone" comes from the Greek tauto for "the same" (which also gives us "tautology") and chronos for "time." The solution, first found by Christiaan Huygens and published in his Horologium oscillatorium (1673), is a cycloid. Thus, if you were to upturn a cycloid, in the manner of an inverted arch, and then release a marble from any point on it, it would take exactly the same time to reach the bottom, no matter where on the curve you started from. Huygens used his discovery to design a more accurate pendulum – one with curved jaws from the point of support that forced the string to follow the right curve no matter how large or small the swing.
The cycloid's unique property is mentioned in the following passage from Herman Melville's Moby Dick: "[The try-pot] is also a place for profound mathematical meditation. It was in the left-hand try-pot of the Pequod, with the soapstone diligently circling round me, that I was first indirectly struck by the remarkable fact, that in geometry all bodies gliding along a cycloid, my soapstone, for example, will descend from any point in precisely the same time."

