folium
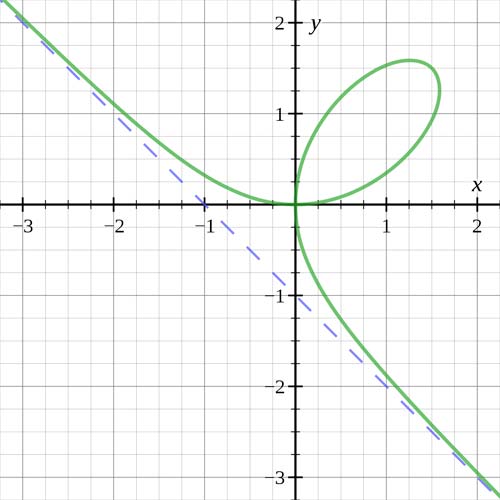
The folium of Descartes (green) with asymptote (blue) when a = 1.
A folium is a curve, first described by Johannes Kepler in 1609, that corresponds to the general equation
(x 2 + y 2)(y 2 + x(x + b)) = 4axy 2, in
Cartesian form, or
r = –b cos θ + 4a cos θ sin2θ, in polar
coordinates.
The Latin folium means "leap-shaped." Three types, known as the simple folium, the bifolium (or double folium), and the trifolium, correspond to the cases when b = 4a, b = 0, and b = a, respectively.
The folium of Descartes is given by the Cartesian equation x 3 + y 3 = 3axy and was first discussed by René Descartes in 1638. Although he found the correct shape of the curve in the positive quadrant, he wrongly thought that this leaf shape was repeated in each quadrant like the four petals of a flower. The problem to determine the tangent to the curve was proposed to Gilles de Roberval who, having made the same incorrect assumption, called the curve fleur de jasmin after the four-petal jasmine bloom – a name that was later dropped. The folium of Descartes has an asymptote x + y + a = 0.


