Neile's parabola

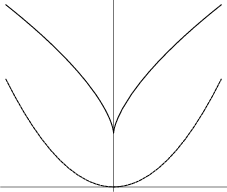
Neile's parabola (upper) and ordinary parabola (lower)

Also known as the semi-cubical parabola, a curve discovered by the English mathematician William Neile (1637–1670) in 1657. It was the first algebraic curve to have its arc length calculated. (Before this, only the arc lengths of transcendental curves such as the cycloid and the logarithmic spiral had been calculated.)

Neile's parabola is described in Cartesian coordinates by the formula

y³ = ax².

Christiaan Huygens showed that this curve satisfies the requirement asked for in 1687 by Gottfried Leibniz, namely, the curve along which a particle may descend under gravity so that it moves equal vertical distances in equal times. Neile's parabola is the evolute of a parabola.

Related category

• PLANE CURVES

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP