trigonometry
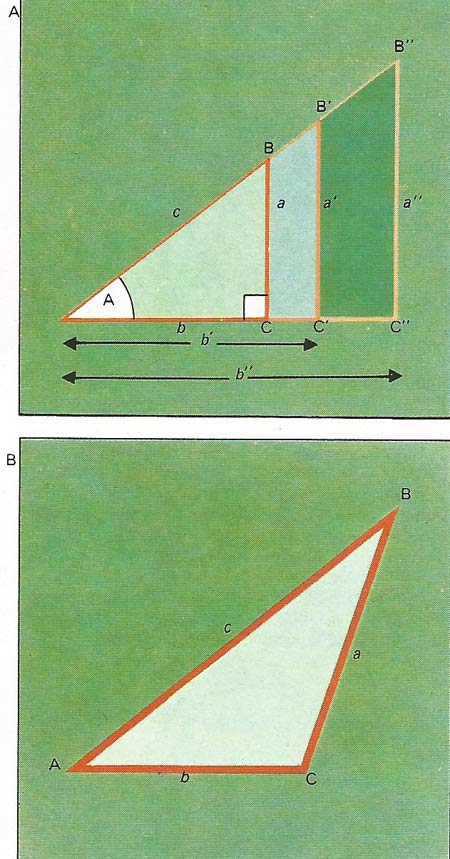
Figure 1. Trigonometry (literally, 'triangle-measuring') is based on six named ratios in a right-angled triangle. Triangles ABC AB'C' and AB"C" [A] all have base angle A. Clearly they have the same relative proportions to a/b - a'/b' = a"/b". In fact any right-angled triangle of base angle A will have this fixed ratio between those sides. It is called the tangent of A or tan A. Thus when A = 45°. The other ratios are: b/a, cotangent (cot A); a/c, sine (sin A); b/c, cosine (cos A); c/b, secant (sec A); c/a, cosecant (cosec A). These are tabulated for all angles; nowadays some pocket calculators can work them out. They will give the dimensions of any triangle, not just right-angled ones, via the formulae [B]: a/sin A = b/sin B = c/sin C and a2 = b2 + c2 – 2bc cos A. (Side a is always opposite angle A, side b opposite angle B, etc.)
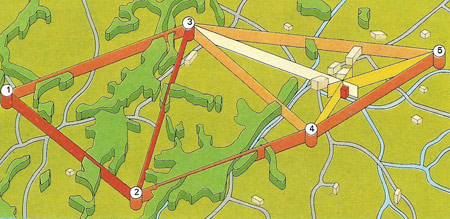
Figure 2. Surveying by triangulation uses the formulae that fix any triangle if one side and two angles are known. Distance [1–2] is carefully measured as the fundamental base line. Reference point [3] is selected and the angles of triangle 123 determined by optical sighting. This fixes point 3 and enables distance 2–3 to be calculated. Sighting from these established reference points will then locate any others [4, 5].
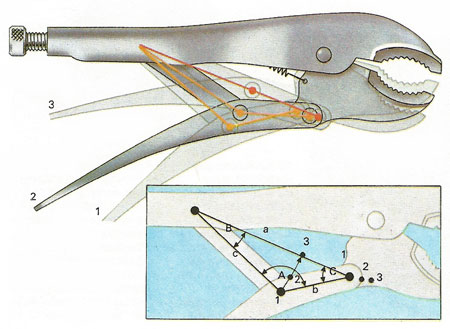
Figure 3. In triangle ABC of the self-grip wrench, a2 – b2 + c2 - 2bc cos A. As b and c are constant lengths a2, and hence a, change only with the cos A term. Reducing A increases cos A and hence a, closing the jaws. When A is large, a small decrease increases cos A substantially. But as A approaches 0°, cos A is near its limit of 1 and changes little. The final closure moves the jaws slightly giving a big leverage ratio with gripping force.

Figure 4. A bent strip (above) does not adopt a sine-wave form but a related "sine-generated" curve. The direction of the strip from point to point varies sinusoidally with distance along the strip. This minimizes the energy of bending stored in the steel. This curve is created on a grand scale (below) when a slow-moving river winds to the sea. The water has little energy and so seeks the line of least resistance as it cuts its channel.

Figure 5. Meandering river.

Figure 6. The quadrant was an early instrument used by astronomers to find the altitude of the heavenly bodies. The surveyor's quadrant developed as a portable version for surveying and artillery ranging. This example was made by Jacob Lusuerg of Rome in 1674. Its most interesting feature is the Vernier scale – invented by Pierre Vernier (c.1580–1637) in 1631 – for measuring to 1/60*. This is the lower arc-scale joining the legs of the pivoting V-shaped unit which slides over the static quadrant base plate. Another scale shows the tangent of measured angle.
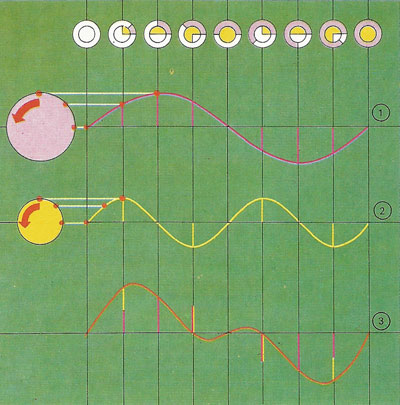
Figure 7. As a rotating radius sweeps out an ever increasing angle, the angle's sine varies cyclically, repeating itself for every additional 360° of rotation. For a circle of unit radius the sine is the height of the end of the radius above the horizontal. Such sinusoidal waveforms occur in vibrations. The frequency is the number of radius-rotations per second. Two simultaneous sine-waves of different frequency will add together to a complex waveform: thus sine-waves [1] and [2] add to give the waveform [3]. which might represent the variation in sound-pressure of two notes sounding together.
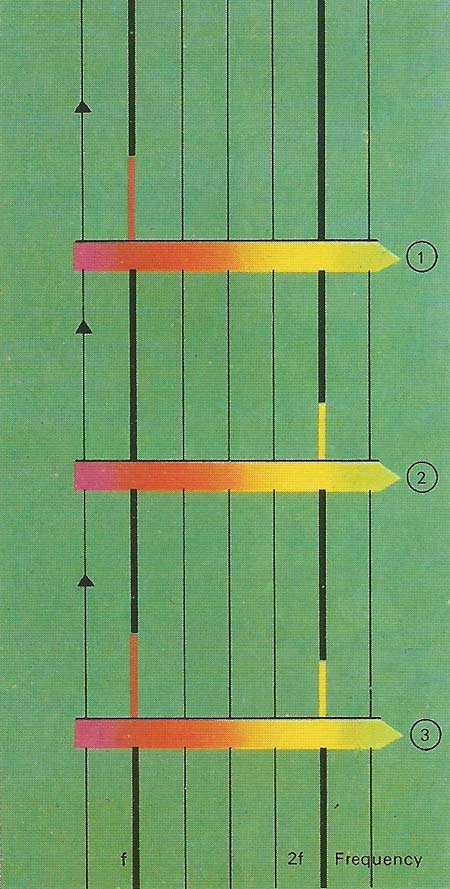
Figure 8. A waveform can be made by combining sine waves; it can also be broken down into them. This diagram here shows the amplitude (intensity) spectra of the waveforms of previous illustration. Waveform 1 has only one component in its spectrum, at the frequency f. Waveform 2 has a single component of frequency 2f but of lower intensity. Their combination [3] has both these lines in its spectrum.
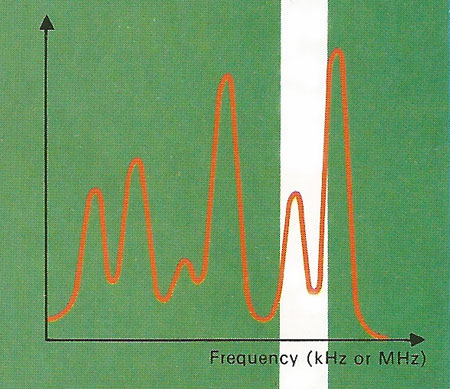
Figure 9. The complex waveform of all the signals entering the radio receiver's antenna will have many components in its frequency spectrum. Each peak is a broadcast on a specific frequency. Some stations are weak, some strong; tuning the radio moves a narrow frequency-acceptance band along the frequency scale to select just one of them. The small modulation is then decoded to give sound.
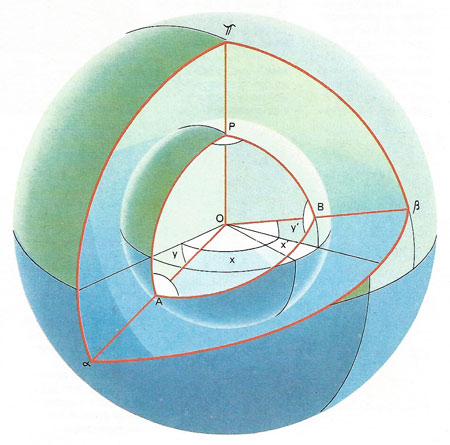
Figure 10. On a sphere such as the Earth any distance can be represented by the angle it makes at the center. Thus distance PB may be represented by angle POB. Accordingly positions are defined by angles of latitude (with the equator) and of longitude (north/south line). Point A has longitude x° west, latitude y° south; B has x'° east y'° north. The spherical trigonometry of spherical triangles such as PAB tells a navigator the distance AB and the compass bearing (angle A) of the journey. Similarly in mapping the heavens astronomers locate stars on spherical celestial triangles like παβ.
Trigonometry is the branch of mathematics that deals with the relationships between the sides and the angles of triangles and the calculations based on them, particularly the trigonometric functions (see below). Sherlock Holmes relies on a little trigonometry to solve a 250-year-old mystery known as the Musgrave Ritual (in a short story of the same name) – an enigmatic series of clues that refers to the shadow of an elm tree when the sun is just visible at the top of a nearby oak to point toward buried treasure. The great detective recalls to Watson his conversation with Reginald Musgrave:
"Have you any old elms?" ...
"There used to be a very old one over yonder, but it was struck by lightening
ten years ago, and we cut down the stump."
"You can see where it used to be?"
"Oh, yes." ...
"I suppose it is impossible to find out how high the elm was?"
"I can give it you it at once. It was sixty-four feet.... When my old
tutor used to give me an exercise in trigonometry, it always took the
shape of measuring heights." ...
I went with Musgrave to his study and whittled myself this peg, to which
I tied this long string with a knot at each yard. Then I took two lengths
of a fishing-rod, which came to just six feet... The sun was just grazing
the top of the oak. I fastened the rod on end, marked out the direction
of the shadow.... It was nine feet in length. Of course, the calculation
was now a simple one. If a rod of six feet threw a shadow of nine, a tree
of sixty-four feet would throw one of ninety-six... I measured out the
distance ... and I thrust a peg into the spot.
History
Trigonometry began as the study of geometrical angles and the information that we may infer from them. As it developed, it became essential in astronomy, land surveying, mapmaking, and building design (notably Egypt's pyramids); later it became vital in technologies as varied as radar and atomic energy.
The earliest known trigonometer was the Greek astronomer and mathematician Hipparchus, who developed trigonometric tables primarily in the service of his work in astronomy. Prior to Hipparchus, trigonometry was not a recognized branch of mathematics: for example, Pythagoras had talked of arithmetic, geometry, harmonics, and astronomy. The earliest surviving work on trigonometry, and also the only surviving comprehensive ancient treatise on astronomy , is the Almagest (c. 150 AD), by the Roman astronomer and citizen of Egypt Claudius Ptolemy.
In the 16th century the emergence of symbolic algebra and the invention of analytic geometry gave trigonometry a vast new range of applications: it became essential in the construction of accurate clocks, navigational equipment, and high-grade musical instruments. In a crucial development, Galileo used trigonometry to calculate the horizontal and vertical movement of a projectile, thus giving rise to the new science of ballistics.
Sines, cosines and tangents
Trigonometry is the art of calculating the dimensions of triangles. The basic idea is that the ratios between the sides of a right-angled triangle depend on its base angle. The ratios have been named the sine of A(sin A), the cosine of A (cos A), the cosine of A (tan A) and others (Figure 1). They have been tabulated for many values of the angle A. Sin A is the length of the triangle side opposite the angle A divided by the longest side; cos A is the length of the side adjacent to the angle A divided by the longest side; and tan A is the ratio of the length of the opposite and adjacent sides of the triangle.
Armed with trigonometrical tables anyone can determine the dimensions of any triangle with great accuracy (Figure 2). Since nearly any shape can be broken up into a series of triangles this is a powerful method of solving even complex spatial problems. To use it in tunnelling engineers set up a station from which both the ends are visible or (as this may be difficult with mountains all around) a station from which other stations are visible, from which in turn the ends can be seen. They measure the angles between all the stations by optical sighting and thus relate the two ends. Trigonometry then tells them the tunnelling angles that will align the two headings. The required accuracy of a thousandth of a degree implies a certain expertise; but the mathematical principle involved is nevertheless extremely simple.
Trigonometric functions
A trigonometric function is any of the functions sine (sin), cosine (cos), tangent (tan), secant (sec), cosecant (cosec), or cotangent (cot), or their inverses, sin –1, etc., which deal with certain proportions in right-angled triangles. The plane curve generated by a trigonometric function is called a trigonometric curve.
 |
Trigonometry in everyday life
Trigonometrical ratios have escaped from their simple geometrical interpretation and uses in surveying and measuring, and now crop up in all sorts of mathematical problems that do not seem to be at all "angular". Some of their most fruitful applications are in circuit theory, radiation physics and information-handling, in which the angles are not real but introduced merely for convenience.
An engineering application
The Simplon Tunnel, between Italy and Switzerland, is 20 kilometers (about 12 miles) long and was bored from both ends through the Alps. When the headings met in the middle, in 1906, they were in exact horizontal alignment and only 10 centimeters (4 inches) out vertically. The engineers managed to smooth out the discontinuity. Using trigonometry they had set up their machines to cut along the 10 kilometers (6 miles) sides of two huge triangles in the mountain.
The sine of 0° is 0 and it increases with increasing angles up to 90°, whose sine is 1. Between 90° and 180° the sine reduces again to 0. From 180° to 270° the sine is negative, decreasing to –1. And from 270° to 360° the sine increases again from –1 to 0. Thus if a trigonometrical angle is regarded as winding up continuously, its sine swings between +1 and –1 and back at each revolution of 360°. This periodic behaviour gives mathematicians a framework for handling waves, vibrations, oscillating radiation such as light and radio waves, and alternating current (AC) electricity. In most European countries a power station generator spins at 50 revolutions a second. As a result its output voltage (which depends on the sine of the angle of rotation) swings back and forth between positive and negative at 50 cycles per second (50 hertz) to generate mains-frequency AC. Any other source of oscillation, even light with a frequency of 600 million million hertz, can be similarly assigned a notional "phase angle" winding up at the appropriate rate of time.
Any vibration, however complicated, can be made up of a set of sine-wave components (or cosine-wave ones which are similar), each with its own frequency. Each frequency is quite independent of the rest. (Two stones thrown into water together generate two sets of spreading ripples which intersect and go right through each other, emerging quite unaffected.) Similarly, the human ear can pick out the notes in a chord although they make a single vibrational pattern in the air or a single groove on a gramophone record.
Angles in a radio beam
Many electronic techniques process these frequency components of vibrations in ways governed by trigonometry. An AM (amplitude modulated) radio transmitter, for example, has to take a sine-wave audio frequency A (say the musical note A, 440 Hz) and attach it somehow to a radio sine-wave "carrier" C, being broadcast at perhaps one million hertz (1 megahertz, in the medium-wave band). It does this in effect by multiplying the audio voltage at each instant by the carrier voltage at the instant and transmitting the result. Now one of the many trigonometriical formulae for simple angles asserts that sin A × sin C = ½cos(A – C) – ½cos (A + C). Since A and C are phase-angles of an audio and carrier frequencies the result of the multiplication is two cosine-waves (just like sine-waves), one at (1,000,000 – 440) hertz and the other at (1,000,000 + 440) hertz, each of half the intensity of the original carrier.
The splitting of the carrier into two closely spaced "sidebands" is called amplitude modulation, or AM. A transmission generally has many such pairs of sidebands continuously changing in their spacing and intensity with the changing frequency-components of the audio signal. At the receiver the audio signal is recovered by the reverse process of the demodulation. It may seem incredible that a mathematical formula first proved for static triangles on paper can be impudently applied to the imaginary rotating angles of an electronic signal.


