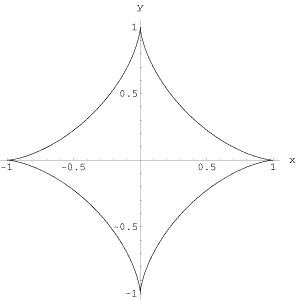
An astroid is a hypocycloid – the path of a point on a circle rolling inside another circle – for which the radius of the inner circle is four times smaller than that of the larger circle; this ratio results in the astroid having four cusps. The astroid was first studied by the Danish astronomer Ole Römer in 1674, in his search for better shapes for gear teeth, and later by Johann Bernoulli (1691), Gottfried Leibniz (1715), and Jean d'Alembert (1748). Its modern name comes from the Greek aster for "star" and was introduced in a book by Karl Ludwig von Littrow published in Vienna in 1836; before this, the curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle.

 

The astroid has the Cartesian equation:

    x ^2/3 + y ^2/3 = r ^2/3

 

where r is the radius of the fixed outer circle, and r/4 is the radius of the rolling circle. Its area is 3πr ²/8, or 3/2 times that of the rolling circle, and its length is 6r.

 

The astroid is a sextic curve and also a special form of a Lamé curve. It has a remarkable relationship with the quadrifolium (a special case of the rose curve): the radial, pedal, and orthoptic of the astroid are the quadrifolium, while the catacaustic (see caustic curve) of the quadrifolium is the astroid. The astroid is also the catacaustic of the deltoid and the evolute of the ellipse.