catenary

Figure 1. A catenary formed by a hanging chain.
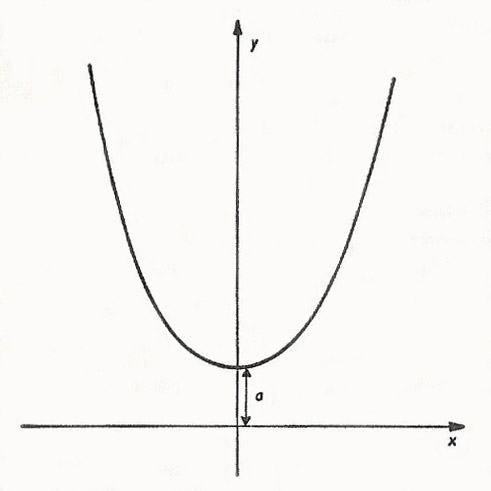
Figure 2. The graph of y = a(ex/a + e-x/a)/2.

Figure 3. A catenoid.
A catenary is the shape that a rope or telephone cable makes, under the influence of gravity, when suspended between two points (Figure 1). The word comes from the Latin catena, meaning "chain," and was first used by Christiaan Huygens while studying the form of suspended chains.
Galileo thought the shape would be a parabola. In fact, near the vertex a parabola and a catenary do look very similar. When x is slightly greater than three however, the catenary begins to rapidly outgrow the value of the parabola. The two shapes are related in another way. If a parabola is rolled along a straight line, the focus of the parabola moves along a catenary curve. Surprisingly, too, if a bicycle with square (or any polygon-shaped) wheels is ridden along a road made of upturned catenaries the wheels will roll smoothly and the rider will stay at the same height! Another remarkable property of the catenary is that its center of gravity is lower than that of any curve of equal perimeter, and with the same fixed points for its extremities.
The St. Louis Arch, which is 630 feet (192 meters) wide at the base and 630 feet tall, follows the form of a catenary, the exact formula for which is displayed inside the arch: y = 68.8 cosh (0.01x – 1), where cosh is the hyperbolic cosine function.
The general equation of a catenary can be written
y =a cosh(x/a),
where a is a constant, or, in terms of the exponential function (see Fig 2),
y = a(ex/a + e-x/a)/2.
See also calculus of variations.
Catenoid
A catenoid is the surface of revolution produced when a catenary rotates about its central axis (Figure 3). The catenoid was first described by Leonhard Euler in 1740 and is the oldest known minimal surface (a shape of least area when bounded by a given closed space). It is the minimal surface connecting two parallel circles of unequal diameter on the same axis; soap film between two circular rings takes this form (see bubbles).
The catenoid is the only known minimal surface that is also a surface of revolution, and is one of only four minimal surfaces that have the topological properties of being unbounded, embedded, and non-periodic; the others are the simple plane, the helicoid, and Costa's surface.

