The center of gravity is the point from which the gravitational attraction of a body appears to act. In a uniform gravitational field this is coincident with the body's center of mass. In a distributed mass, the center of gravity (CG) is an appropriately defined "average location" of its parts. If the mass is a rigid body subject to the Earth's gravity, then if it is supported at the CG it will stay balanced and not tilt to any side. In a system subject only to internal forces, the CG always stays in the same spot; hence the Earth-Moon system rotates around its mutual CG (not around Earth's center), and a rocket flies forward when it ejects a high-speed stream of gas backward. For an expanded body or collection of particles subject to gravitation, the CG is the point through which the resultant force of gravity acts, regardless of the orientation of the body.

 

Determining the center of gravity

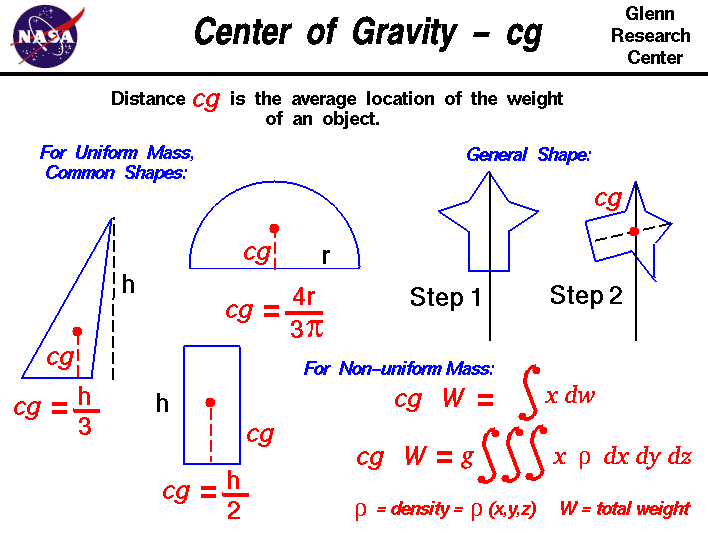
In general, determining the center of gravity is a complicated procedure because the mass (and weight) may not be uniformly distributed throughout the object. The general case requires the use of calculus which we will discuss later. If the mass is uniformly distributed, the problem is greatly simplified. If the object has a line (or plane) of symmetry, the CG lies on the line of symmetry. For a solid block of uniform material, the center of gravity is simply at the average location of the physical dimensions. (For a rectangular block, 50 × 20 × 10, the center of gravity is at the point (25, 10, 5).) For a triangle of height h, the CG is at h/3, and for a semicircle of radius r, the CG is at (4r/(3π)) where π is ratio of the circumference of the circle to the diameter. There are tables of the location of the center of gravity for many simple shapes in math and science books. The tables were generated by using the equation from calculus shown in the diagram.

 

For an object of general shape, there is a simple mechanical way to determine the center of gravity:

 

1. If we just balance the object using a string or an edge, the point at which the object is balanced is the center of gravity. (Just like balancing a pencil on your finger!)

 

2. Another, more complicated way, is a two-step method illustrated above. In Step 1, you hang the object from any point and you drop a weighted string from the same point. Draw a line on the object along the string. For Step 2, repeat the procedure from another point on the object You now have two lines drawn on the object which intersect. The center of gravity is the point where the lines intersect. This procedure works well for irregularly shaped objects that are hard to balance.

 

If the mass of the object is not uniformly distributed, we must use calculus to determine center of gravity. The center of gravity can be determined from:

 

    CG × W = ∫ x dw

 

where x is the distance from a reference line, dw is an increment of weight, and W is the total weight of the object. To evaluate the right side, we have to determine how the weight varies geometrically. From the weight equation, we know that:

 

    w = m × g

 

where m is the mass of the object, and g is the gravitational constant. In turn, the mass m of any object is equal to the density, ρ (rho), of the object times the volume, V:

 

    m = ρ × V

 

We can combine the last two equations:

 

    w = g × ρ × V

 

then

 

    dw = g × ρ × dV

 

    dw = g × ρ(x,y,z) × dx dy dz

 

If we have a functional form for the mass distribution, we can solve the equation for the center of gravity:

 

    CG × W = g × ∫∫∫ x × ρ(x,y,z) dx dy dz

 

where ∫∫∫ indicates a triple integral over dx, dy, and dz. If we don't know the functional form of the mass distribution, we can numerically integrate the equation using a spreadsheet. Divide the distance into a number of small volume segments and determining the average value of the weight/volume (density times gravity) over that small segment. Taking the sum of the average value of the weight/volume times the distance times the volume segment divided by the weight will produce the center of gravity.