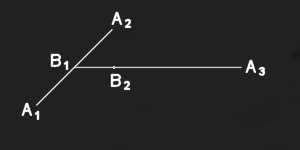
The center of mass is the point at which a system of masses would balance if placed on a pivot. If m₁ and m₂ are the masses of two particles placed at the points A₁ and A₂, and if the line A₁ A₂ is divided at B₁, so that m₁ A₁ B₁ = m₂ A₂ B₁, the point B₁ is the center of mass of the two particles. If m₃ is a third mass at A₃, and if B₁ A₃ is divided at B₂, so that (m₁ + m₂) = m₃ (A₃ B₂), B₂ is the center of mass of the three particles. In general, if there are any number of particles, a continuation of the above process will enable us to find their center of mass. Every body may be supposed to be made up of a very large number of particles connected by cohesion. From this it is clear that the center of mass is a definite point for every piece of matter.

 

In general, the determination of the center of mass requires the use of integral calculus. In the case of some bodies, such as those which have a simpler geometric form and are of uniform density, elementary mathematical methods will generally suffice. Any straight line or plane that divides a homogeneous body symmetrically must contain its center of mass. This can be understood because the particles of the body may be arranged in pairs of equal mass and at equal distance from the line or plane; and, since the center of mass of each pair lies in the line or plane, the center of mass of the whole must also lie in the same line or plane. For example, the center of mass of a uniform thin straight rod is the middle point; that of a uniform rod bent in the form of a parallelogram, the point of intersection of its diagonals; that of a lamina, uniform in thickness and density and in the form of a circle, ellipse, or parallelogram, its center of figure; that of a homogenous sphere, its center; that of a parallelepiped, the intersection of its diagonals; that of a circular cylinder with parallel ends, the middle point of its axis.

An important case is that of a uniformly thin triangular plate. Let ABC be the plate. Bisect AB at P and join CP. Let the triangle be divided by right lines parallel to AB into an indefinitely large number of indefinitely narrow strips. The center of mass of each strip is its middle point. But all the middle points lie on CP. The center of mass of the whole plate must therefore lie on CP. Again, if BC is bisected at Q, and AQ are joined, the center of mass of the whole plate must lie in AQ. The center of mass must therefore be O, the point of intersection of CP and AQ. It is easily proved by elementary geometry that OP = one-third of CP. Hence, the center of mass of a triangular plate is obtained by joining a vertex to the middle point of the opposite side and taking the point two-thirds of this line measured from the vertex. By a similar method the center of mass of other plane figures may be obtained.

 

In the case of a single mass, the center of gravity, for the sake of simplicity of calculations, is the point at which it can be assumed all the mass is concentrated. In a binary star system, the center of mass would lie nearer to the more massive component.