squaring the circle
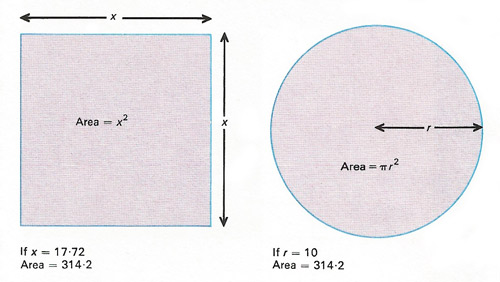
Although drawing a square with exactly the same area as a given circle is impossible, an approximate solution is possible using algebra. The area of a circle of radius r is πr 2 and of a square of side r is r 2. For equal areas πr 2 = x 2, or x = r√π. If r = 10, x = √314.2, which equals 17.72 approximately. A square of side 17.72 cm has an area almost exactly the same as a circle of radius 10 cm.
The problem of squaring the circle is to find a construction, using only a straight-edge and compass, that would give a square of the same area as a given circle. It is now known that this is impossible because, as the German mathematician Ferdinand von Lindemann showed in 1882, it would amount to finding a polynomial expression for π, which can't be done as π is a transcendental number. (All the coordinates of all points that can be constructed with ruler and compass are algebraic numbers.)
This minor inconvenience, however, hasn't prevented some amateur mathematicians from continuing to claim they have found proofs that the circle can be squared. Some of the most bizarre attempts have involved proposing a different and rational value for π. In 1897, the Indiana State Legislature came within a hair's breadth of introducing a bill to set the value of π equal to 3! In fact, long before π was finally proved to be transcendental most learned societies had conjectured that a proof was impossible and had stopped considering circle-squaring arguments sent to them.

