Dürer, Albrecht (1471–1528)

Albrecht Dürer, self-portrait.
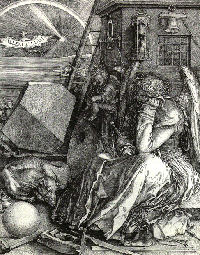
Dürer's Melancholia.
...sane judgment abhors nothing so much
as a picture perpetrated with no technical knowledge, although with plenty
of care and diligence. Now the sole reason why painters of this sort are
not aware of their own error is that they have not learnt Geometry, without
which no one can either be or become an absolute artist...
Dürer (The Art of Measurement, 1525)
Albrecht Dürer was a German printmaker who, through applying mathematics to art, brought important ideas to mathematics itself especially in the area of perspective geometry.
Dürer was born in Nüremberg, one of 18 children, and showed an early talent for art. After a four-year apprenticeship in painting and woodcutting, he began traveling around Europe, especially Italy, in search of new styles and ideas. Back in Nüremberg, he began a serious study of mathematics, absorbing Elements by Euclid and De architectura by the great Roman architect Vitrivius, and studying the work of Leone Alberti (1404–1472) and Luca Pacioli on mathematics and art, in particular their work on proportion. His mastery of perspective is clear in woodcuts "Life of a Virgin" (1502–1505). In about 1508 Dürer began to collect material for a major work on mathematics and its applications to the arts. This work would never be finished but Dürer did use parts of the material in later published work. One of his most famous engravings "Melancholia," produced in 1514, contains the first magic square to be seen in Europe, cleverly including the date 1514 as two entries in the middle of the bottom row. Also of mathematical interest in Melancholia is the polyhedron in the picture, the faces of which appear to consist of two equilateral triangles and six somewhat irregular pentagons. In 1825 Dürer published a four-volume treatise, Underweysung der Messung (available in English translation as Painter's Manual), which dealt with, among other things, the construction of various curves, polygons, and other solid bodies. One of the first books to teach the methods of perspective, it was highly regarded throughout the 16th century and presents the earliest known examples of polyhedral nets, i.e., polyhedra unfolded to lie flat for printing.
Dürer traveled to Italy to learn about perspective and was keen to publish the methods so they weren't kept secret among a few artists. Whom he learned from is not known, but Luca Pacioli is a likely possibility. Some of the techniques and illustrations also follow closely the work of Piero della Francesca.
One of Dürer's masterpieces, the woodcut Melancholia I, features a frustrated thinker sitting by a polyhedron that consists of a cube or rhombohedron that has been truncated at the upper vertex. (It is impossible to tell if the lower vertex is also truncated, so that the solid rests on a triangular face, or if the lower vertex symbolically penetrates the earth, though the latter possibility is not often considered.) It is possible to proportion it so that the vertices project onto a 4-by-4 square grid like that of the magic square.
Dürer's final work, his Treatise on Proportion, was published posthumously and laid the groundwork for descriptive geometry and its rigorous mathematical treatment by Gaspard Monge.


