Pascal, Blaise (1623–1662)

Figure 1. Pascaline.

Figure 2. Blaise Pascal.
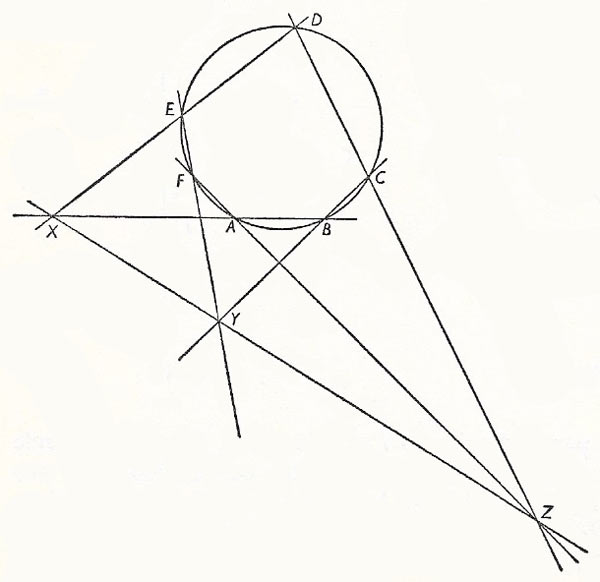
Figure 3. Pascal's theorem. Opposite sides are: AB and DE, BC and EF, and CD and FA.

Figure 4. Pascal's triangle.
Blaise Pascal was a French mathematician, philosopher, physicist, and pioneer of probability theory whose short life was rich with mathematical invention but whose name, ironically, is most familiar from its association with an array of numbers – Pascal's triangle – which he didn't discover (though he did important work on it). Educated by his father (after whom the limaçon of Pascal is named), Pascal showed his intellectual prowess early on by proving one of the most important theorems in projective geometry at the age of 16. Three years later he devised the world's second mechanical calculating machine (the first was made by Wilhelm Schickard in 1623) to help with his father's business; he sold about 50 of these "Pascalines," several of which survive.
Pascal's studies of the cycloid inspired others to develop the calculus. His experiments (performed by his brother-in-law) observing the heights of a column of a barometer at different altitudes on the mountain Puy-de-Dôme (1646) confirmed that the atmospheric air had weight. He also pioneered hydrodynamics and hydrostatics, in doing so discovering Pascal's law.
In 1654, he and Pierre de Fermat, in an exchange of correspondence, laid the foundation for the theory of probability. They considered the dice problem, already studied by Girolamo Cardano, and the problem of points also considered by Cardano and, around the same time, by Luca Pacioli and Niccolò Tartaglia. The dice problem asks how many times one can expect to throw a pair of dice before getting a double six; the problem of points asks how to divide the stakes if a game of dice is incomplete. Pascal and Fermat solved the problem of points for a two-player game but didn't develop powerful enough methods to solve it for three or more players.
In the same year, Pascal was almost killed in an incident in which the horses pulling his carriage bolted and the carriage was left hanging over a bridge above the river Seine. Though rescued unharmed, he shortly after converted to the rigorous Jansenist sect of the Catholic Church. His philosophical work Pensées, written between 1656 and 1658 contains his famous argument, often called Pascal's wager, for belief in God. Having suffered poor health for most of his adult life, he died in great pain of cancer at the age of 39.
Pascal and his calculating machine
Pascal's machine consists of a box containing six sets of pinwheels and cylinders. Each cylinder bears the figures 0–9 around its edge, and is so arranged that only one figure – equivalent to 1/10 of the circumference – can be seen through the sighthole at any given time. The pinwheels are connected to the six horizontal dials (rather like an old telephone dial and marked from 0–9) at the front, so that when the dial is turned, the corresponding pinwheel and cylinder turn with it.
To follow the method of using the Pascaline, suppose that the operator wishes to add together the numbers 2, 5, and 3. With a stylus or peg he turns the right hand dial anticlockwise from where the figure 2 is marked round to 0. The dial moves in the opposite direction to the dial on a telephone and it does not spring back to its starting position when the peg is removed. This action turns the pinwheel and hence the cylinder 2/10 of a revolution from 0 to 2. The operator now repeats the process, this time "dialing" 5. The pinwheel turns the cylinder a further 5/10 of a revolution, so that the total registered there is 7. One again he dials a number, in this example number 3. The pinwheel moves through 3/10 of a turn, as does the cylinder. Because the cylinder is marked in tenths, however, and ten units have been added (2 + 5 + 3), this brings it round to 0 again. A trip mechanism within the calculator, however, "carries" the figure 1 to the cylinder immediately to the left, i.e., it turns the next wheel 1/10 of a revolution, from 0 to 1. There are six cylinders altogether, which represent (from left to right) single figures, tens, hundreds, thousands, ten thousands and hundreds of thousands, respectively. The adding of the single figures 2, 5, and 3 gives 0 in the single figure cylinder and 1 on the tens cylinder, thus producing the answer total 10. With the six cylinders, sums can be added up to a total of 999,999. In fact some Pascalines have two sets of numbers on the dials and the cylinders, the second set running in the reverse direction (i.e., from 9–0 instead of 0–9). The latter can be used for subtraction, and are covered up on the cylinders by a sliding strip of metal when not in use.
Some of Pascal's machines were designed for adding livres, sous, and deniers (the contemporary French currency), and may be regarded as the forerunners of modern cash registers.
Pascal's law
In hydrostatics, Pascal's law is a law which states that the pressure in an enclosed body of fluid arising from forces applied to its boundaries is transmitted equally in all directions with unchanged intensity. This pressure acts at right angles to the surface of the fluid container.
Pascal's mystic hexagon
If a hexagon ADBFCE (not necessarily convex) is inscribed in a conic section (in particular a circle), then the points of intersections of opposite sides (AD with FC, DB with CE and BF with EA) are collinear. This line is called the Pascal line of the hexagon. A special case is when the conic degenerates into two lines; the theorem still holds but is then usually called Pascal's theorem (see below) or Pappus' theorem.
Pascal's theorem
The three points of intersection X, Y, and Z of opposite sides of a hexagon inscribed in a circle lie on a straight line (Pascal's line), opposite sides being sides separated from one another by two sides (Figure 3).
Pascal's triangle
Pascal's triangle is an array of numbers in which the individual numbers are the binomial coefficients (Figure 4). The array has the following properties:
1. Each number is the sum of the two numbers standing above it to the left and right; e.g. 10 = 4 + 6.
2. Each number is equal to the sum of all numbers in the left or right diagonal, beginning with the number immediately above to the left or right, and proceeding upwards; e.g. 15 = 5 + 4 + 3 + 2 + 1 and 15 = 10 + 4 + 1.
3. Each diagonal is an arithmetic sequence; e.g.
1st diagonal: 1, 1, 1, 1, 1, 1,... Arithmetic sequence of zero order.
2nd diagonal: 1, 2, 3, 4, 5,... Arithmetic sequence of 1st order.
3rd diagonal: 1, 3, 6, 10, 15,... Arithmetic sequence of 2nd order.
4th diagonal: 1, 4, 10, 20,... Arithmetic sequence of 3rd order.
And so on.
Pascal's wager
Pascal's wager is a logical argument to show that the potential benefits of believing in the Christian God outweigh the potential risks of not doing so. The argument appears in the Pascal's posthumously published Pensées (1670). Pascal assumes that either the Christian God exists or does not, and that each person can decide whether to believe in him or not. If God does not exist, either believing in him not believing in him will result in the same outcome, though the believer may have a happier life than the nonbeliever because the believer can gain comfort from the religion. If God does exist, then believing in him grants the possibility for eternal life, while not believing in him will result in eternal damnation.
Previous thinkers, such as St. Thomas Aquinas and René Descartes, had attempted to prove God's existence through rational, logical proofs, but Pascal took another tack. His focus on the best possible outcome, though it echoed some classical writings, eschewed the previous metaphysical justifications for Christianity, and instead adopted a practical measurement based on the potential outcomes.
Pascal's wager is both a logical argument and an exercise in what would come to be known as decision theory. It makes no attempt at convincing potential believers of the existence of God. Instead, the wager offers a pragmatic approach. Pascal's argument paves the way for other belief systems, such as existentialism, which focus less on metaphysical or spiritual questions in lieu of potential benefits.

