combinatorics

Figure 1. "The art of change ringing is peculiar to the English,
and, like most English peculiarities, unintelligible to the rest of
the world. To the musical Belgian, for example, it appears that the
proper thing to do with a carefully tuned ring of bells is to play
a tune upon it. By the English campanologist ... the proper use of
the bells is to work out mathematical permutations and combinations."
—Dorothy L. Sayers, The Nine Tailors.
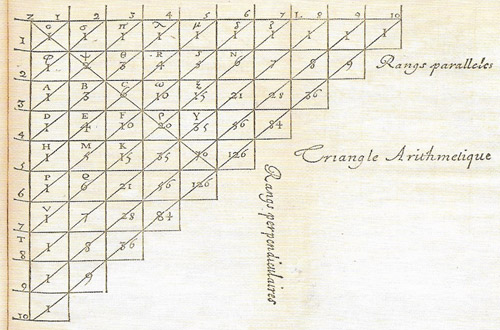
Figure 2. Pascal's triangle.
Combinatorics is the study of the ways of choosing and arranging objects from given collections and the study of other kinds of problems to do with counting the number of ways to do something.
Topics in combinatorics
Bell number
A Bell number is the number of ways that n distinguishable objects (such as differently colored balls) can be grouped into sets (such as buckets) if no set can be empty. For example, if there are three balls, colored red (R), green (G), and blue (B), they can be grouped in five different ways: (RGB), (RG)(B), (RB)(G), (BG)(R), and (R)(G)(B), so that the third Bell number is 5. The sequence of Bell numbers, 1, 2, 5, 15, 52, 203, 877, 4140, 21147,..., can be built up in the form of a triangle, as follows. The first row has just the number one. Each successive row begins with the last number of the previous row and continues by adding the number just written down to the number immediately above and to the right of it.
1 2
2 3 5
5 7 10 15
15 20 27 37 52
52 ...
The Bell numbers appear down the left-hand side of the triangle. These normal Bell numbers contrast with ordered Bell numbers, which count the number of ways of placing n distinguishable object (balls) into one or more distinguishable sets (buckets) The ordered Bell numbers are 1, 3, 13, 75, 541, 4683, 47293, 545835, ...
Bell numbers, named after Eric Temple Bell, who was one of the first to analyze them in depth, are related to the Catalan numbers.
Binomial
A binomial is a polynomial expression containing two terms, joined by + or –. The binomial theorem gives the result of raising a binomial expression to a power; the expansion and the series it leads to are called the binomial expansion and the binomial series. A binomial distribution is described by a formula related to the binomial expansion. A binomial equation is a particular kind of equation that contains two terms. See also functions.
Binomial coefficient
A binomial coefficient is any of the coefficients of the powers of x or y in the expansion (see binomial theorem, below) of (x + y)n.
The binomial coefficient of a typical term x(n – m)ym, written nCm, or (mn), gives the number of ways of picking m unordered outcomes from n possibilities, and is also known as a combination. It has the value n!/(n – m)!m!
The binomial coefficients form the rows of Pascal's triangle.
Binomial theorem
The binomial theorem is a method of expanding the binomial expression (x + y)n into a finite or infinite series of powers of x and y, where n is a number either integral or fractional, positive or negative, rational or irrational; thus
(x + y)n = xn + an-1xn-1y + an-2xn-2y2 + ... + yn
The coefficients ai are called binomial coefficients.
The binomial theorem was discovered by Isaac Newton about 1666, and was first published in 1704 in the second appendix to Newton's Optics. That particular case of the theorem when n is a positive integer was known to mathematicians prior to Newton (e.g., Briggs and Pascal), and Newton himself gave no demonstration of the truth of his theorem.
Catalan number
A Catalan number is any number, un, from the Catalan sequence defined by
un = (2n)! / (n + 1)!n!
The sequence begins: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, ... The values of un represent the number of ways a polygon with n + 2 sides can be cut into n triangles using straight lines joining vertices and are named after the Belgian mathematician Eugène Catalan (1814–1894). They also arise in other counting problems, for example in determining how many ways 2n beans can be divided into two containers if one container can never have less than the second.
Cayley's mousetrap
Cayley's mousetrap is a permutation problem invented by Arthur Cayley. Write the numbers 1, 2, ..., n on a set of cards, and shuffle the deck. Now, start counting using the top card. If the card chosen does not equal the count, move it to the bottom of the deck and continue counting forward. If the card chosen does equal the count, discard the chosen card and begin counting again at 1. The game is won if all cards are discarded, and lost if the count reaches n + 1. The number of ways the cards can be arranged such that at least one card is in the proper place for n = 1, 2, ..., are 1, 1, 4, 15, 76, 455, ...
Change ringing
Change ringing is the ringing of a set of bells in a precise relationship to one another to produce a pleasing sound (Figure 1). Bells are number 1, 2, 3, 4, 5... from lightest (highest-pitched) to heaviest. After each sequence, or round, the order of the bells is changed slightly in a predetermined way. With 5 bells, there are 5 × 4 × 3 × 2 × 1, or 120, possible changes, which take about 4 min to ring. With 6, 7, or 8 bells, the number of unique changes is 720, 5,040, and 40,320, respectively. To produce pleasing variations in the sound, bells are made to change places with adjacent bells in the row, for example:
| 1 2 3 4 5 6 7 8 |
| 2 1 4 3 6 5 8 7 |
These rows are the musical notation of change ringing. No bell moves more than one place in the row at a time, although more than one pair may change in the same row. In order to ring a different row with each pull of the rope, ringers have devised methods for changing pairs in orderly ways. In ringing a method, the bells begin in rounds, ring changes according to the method, and return to rounds without repeating any row along the way. These place changes produce musical patterns, with the sounds of the bells weaving in and out.
Experienced ringers test and extend their abilities by ringing peals: 5,000 or more changes without breaks or repeating a row. Peals customarily last about three hours. The first peal was rung in England in 1715. Chiming bells (swinging them through a short arc using a rope and a lever) goes well back into the Middle Ages, but it wasn't until the 17th century that ringers developed the full wheel, which allowed enough control for orderly ringing. In 1668 Fabian Stedman published Tintinnalogia (The Art of Change Ringing), containing all the available information on systematic ringing. The theory of change ringing set forth by Stedman has been refined in later years but remains essentially unchanged today. Bells for change ringing are hung in stout frames that allow the bells to swing through 360°. Each bell is attached to a wooden wheel with a handmade rope running around it and takes about 2 sec to rotate. The bells are arranged in the frame so their ropes hang in a circle in the ringing chamber below. Into each rope is woven a tuft of brightly colored wool (a sally), which marks where the ringer must catch the rope while ringing. Bells are rung from the "mouth up" position. With a pull of the rope, the bell swings through a full circle to the up position again. With the next pull it swings back in the other direction. The plot of Dorothy Sayers' The Nine Tailors (1934), considered one of her best works, revolves around the art of change ringing.
Combination
A combination is a set of objects selected without reference to the order in which they are arranged. Compare with permutation (below).
Combinatorial analysis
Combinatorial analysis is the branch of mathematics dealing with subdivisions of sets; its primary concerns are combinations and permutations and partitions. A partition of a number n is its expression in the form of a sum of positive integers: i.e., setting
n = a1 + a2 + ... + an.
For example, the number 5 has 7 partitions: (1 + 1 + 1 + 1 + 1), (2 + 1 + 1 + 1), (2 + 2 + 1), (3 + 1 + 1), (3 + 2), (4 + 1), and (5).
By extension combinatorial topology is the study of complex forms in terms of their being built up from combinations of basic geometric forms.
Partition
A partition is a particular ordering of a collection of objects. For example, if an athlete has won three medals, a bronze one (B), a silver one (S), and a gold one (G), there are six ways they can be permuted or lined up: BSG, BGS, SBG, SGB, GBS, and GSB. If six people want to sit on the same park bench, there are 720 ways in which they can organize themselves. In general, n things can be permuted in n × (n – 1) × (n – 2) × ... × 2 × 1 = n! ways (where "!" is the symbol for factorial). How about if there are n distinct objects but we want to permute them in groups of k (where k ≤ n). How many ways can that be done? The first member of the group can be picked in n ways because there are n objects to pick from. The second member can be filled in (n - 1) ways since one of the n elements has already been taken. The third member can be filled in (n – 2) ways since 2 elements have already been used, and so. This pattern continues until there are k things have been chosen. This means that the last member can be filled in (n – k + 1) ways. Therefore a total of n (n – 1)(n – 2) ... (n–k + 1) different permutations of k objects, taken from a pool of n objects, exist. If we denote this number by P(n, k), we can write P(n, k) = n! / (n - k)!
Partition number
A partition number is a number that gives the number of ways of placing n indistinguishable balls into n indistinguishable urns. For example:
1: (*)
2: (**) (*)(*)
3: (***) (**)(*) (*)(*)(*)
5: (****) (***)(*) (**)(**) (**)(*)(*) (*)(*)(*)(*)
7: (*****) (****)(*) (***)(**) (***)(*)(*) (**)(**)(*) (**)(*)(*)(*)
(*)(*)(*)(*)(*)
11: (******) (*****)(*) (****)(**) (****)(*)(*) (***)(***) (***)(**)(*)
(***)(*)(*)(*) (**)(**)(**) (**)(**)(*)(*) (**)(*)(*)(*)(*) (*)(*)(*)(*)(*)(*)
The sequence runs: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, ... If the urns are distinguishable, the number of ways is 2n. If the balls are distinguishable, the number of ways is given by the nth Bell number.
Plane partition
A plane partition is a stack of unit cubes in a rectangular box or in the positive octant in space such that to the left, behind, and below every cube lies either another cube or a wall. A plane partition in a box is equivalent to a lozenge tiling of a hexagon in the plane.
Pascal's triangle
 |
Pascal's triangle (Figure 2) is a triangular pattern of numbers in which each number is equal to the sum of the two numbers immediately above it. Although named after Blaise Pascal, who studied it, this arithmetic triangle has been known about since at least the 12th century and has a variety of other names. In Italy it is called Tartaglia's triangle (after Niccoló Tartaglia) and in many parts of Asia it is referred to as Yang Hui's triangle. Yang Hui was a minor Chinese official who wrote two books, dated 1261 and 1275, which use decimal fractions (long before they appeared in the West) and contain one of the earliest accounts of the triangle; at about the same time, Omar Khayyaam also wrote about it. The Chinese triangle appears again in 1303 on the front of Chu Shi-Chieh's Ssu Yüan Yü Chien (Precious Mirror of the Four Elements), a book in which Chu says the triangle was known in China more than two centuries before his time.
The numbers in Pascal's triangle give the number of ways of picking r unordered outcomes from n possibilities. This is equivalent to saying that the numbers in each row are the binomial coefficients in the expansion of (x + y)n:
(x + y)0 = 1
(x + y)1 = 1x + 1y
(x + y)2 = 1x 2 + 2xy + 1y 2
(x + y)3 =
1x 3 + 3x 2y + 3xy 2 + 1y3
(x + y)4 = 1x 4 + 4x 3y + 6x 2y 2 + 4xy 3 + 1y 4
and so on. In addition, the shallow diagonals of the triangle sum to give the numbers in the Fibonacci sequence.
Pascal's triangle also has the following properties:
• Each number is the sum of the two numbers standing above it to the left and right; e.g. 10 = 4 + 6.
• Each number is equal to the sum of all numbers in the left or right diagonal, beginning with the number immediately above to the left or right, and proceeding upwards, e.g. 15 = 5 + 4 + 3 + 2 + 1 and 15 = 10 + 4 + 1.
• Each diagonal is an arithmetic sequence; e.g.
1st diagonal: 1, 1, 1, 1, 1, ... (arithmetic sequence of zero order)
2nd diagonal: 1, 2, 3, 4, 5, ... (arithmetic sequence of 1st order)
3rd diagonal: 1, 3, 6, 10, 15, ... (arithmetic sequence of 2nd order)
4th diagonal: 1, 4, 10, 20, ... (arithmetic sequence of 3rd order)
and so on.
Ramsey theory
Ramsey theory is a branch of mathematics that asks questions such as: Can order always be found in what appears to be disorder? If so, how much can be found and how big a chunk of disorder is needed to find a particular amount of order in it? Ramsey theory is named after the English mathematician Frank P. Ramsey (1904–1926) who started the field in 1928 while wrestling with a problem in logic. (Frank's one-year-younger brother, Arthur, served as Archbishop of Canterbury from 1961 to 1974.) His life was cut short in 1930, at the age of 26, following a bout of jaundice. Ramsey suspected that if a system was big enough, even if it seemed to be disorderly to an arbitrary degree, it was bound to contain pockets of order from which information about the system could be gleaned. See also chaos, complexity, and dynamical systems.
Schoolgirls problem
The schoolgirls problem A problem in combinatorics posed by the Thomas Kirkman in 1847:1
A school mistress has fifteen girl pupils and she wishes to take them on a daily walk. The girls are to walk in five rows of three girls each. It is required that no two girls should walk in the same row more than once per week. Can this be done?In fact, provided n is divisible by 3, we can ask the more general question about n schoolgirls walking for (n - 1)/2 days so that no girl walks with any other girl in the same triplet more than once. Solutions for n = 9, 15, and 27 were given in 1850 and much work was done on the problem thereafter. It is important in the modern theory of combinatorics.
1. Kirkman, T. P. "On a Problem in Combinatorics." Cambridge and Dublin Math. J., 2: 191–204 (1847).
Thirty-six officers problem
The thirty-six officers problem is to arrange 36 officers in a 6 × 6 square so that one officer from each of six regiments appears in each row and one from each of six ranks appears in each column. This problem, first posed by Leonhard Euler in 1779, is equivalent to finding two mutually orthogonal Latin squares of order six. Euler correctly conjectured that there was no solution; the search for a proof led to important developments in combinatorics.


