Apollonius of Perga (c. 262–c. 190 BC)

Figure 1. Apollonius of Perga.
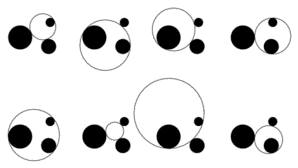
Figure 2. Apollonius circles.
Apollonius of Perga was a highly influential Greek mathematician and astronomer, born in a region of what is now Turkey, who became known as the "Great Geometer." In his famous eight-part work On Conics, he introduced such terms as "ellipse," "parabola," and "hyperbola" – the conic sections that, as we now know, describe the shapes of various types of orbit. Euclid and others had written earlier about the basic properties of conic sections but Apollonius added many new results, particularly to do with normals and tangents to the various conic curves. In particular, he showed that the conic curves can be obtained by taking plane sections at different angles through a cone.
Apollonius also helped found Greek mathematical astronomy. Ptolemy says in his Syntaxis that Apollonius introduced the theory of epicycles to explain the apparent motion of the planets across the sky. Although this isn't strictly true, since the theory of epicycles was mooted earlier, Apollonius did make important contributions, including a study of the points where a planet appears stationary. He also developed the hemicyclium, a sundial with hour lines drawn on the surface of a conic section to give greater accuracy. See also Greek astronomy.
One of the most famous questions he raised is known as the Apollonius problem (see below). He also wrote widely on other subjects including science, medicine, and philosophy. In On the Burning Mirror he showed that parallel rays of light are not brought to a focus by a spherical mirror (as had been previously thought) and he discussed the focal properties of a parabolic mirror. A few decades after his death, the Emperor Hadrian collected his works and ensured their publication throughout his realm.
Apollonius problem
The Apollonius problem is: given three objects in the plane, each of which may be a circle C, a point P (a degenerate circle), or a line L (part of a circle with infinite radius), find another circle that is tangent to (just touches) each of the three. This problem was first recorded in Tangencies, written around 200 BC by Apollonius and so is named after him.
There are ten cases: PPP, PPL, PLL, LLL, PPC, PLC, LLC, LCC, PCC, CCC (Fig 2). The two easiest involve three points or three straight lines and were first solved by Euclid. Solutions to the eight other cases, with the exception of the three-circle problem, appeared in Tangencies; however, this work was lost. The most difficult case, to find a tangent circle to any three other circles, was first solved by the French mathematician François Viète (1540–1603) and involves the simultaneous solution of three quadratic equations, although, in principle, a solution could be found using just a compass and a straightedge.
Any of the eight circles that is a solution to the general three-circle problem is called an Apollonius circle. If the three circles are mutually tangent then the eight solutions collapse to just two, which are known as Soddy circles. If, having started with three mutually tangent circles and having created a fourth – the inner Soddy circle – that is nested between the original three, the process is repeated to yield three more circles nested between sets of three of these, and then repeated again indefinitely, fractal is produced. The points that are never inside a circle form a fractal set called the Apollonian gasket, which has a fractional dimension of about 1.30568.

