lemniscate of Bernoulli
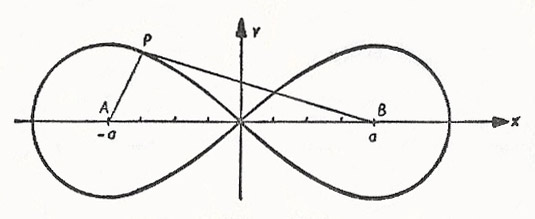
Graph of the lemniscate with equation (x 2 + y 2)2 = 2a 2(x 2 – y 2).
The lemniscate of Bernoulli, also known simply as a lemniscate, is a curve 'shaped like a figure 8, or a knot, or the bow of a ribbon' in the words of Jacob Bernoulli in an article published in 1694. Bernoulli named the curve "lemniscate" after the Greek lemniskus for a pendant ribbon (the type fastened to a victor's garland). It has the Cartesian equation
(x 2 + y 2)2 = 2a 2(x 2 – y 2)
At the time he wrote his article, Bernoulli wasn't aware that the curve he was describing was a special case of a Cassinian oval, which had been described by Cassini in 1680. The lemniscate and the Cassinian ovals are obtained by taking two points A and B symmetrically placed with respect to the origin and distance 2a apart, and determining points P such that PA × PB = constant (= b 2). If a = b, we have the lemniscate (see the diagram); if b > a the Cassinian oval lies outside and encloses the lemniscate; if b < a the curve lies wholly within the two loops of the lemniscate. The equation of the Cassianian ovals is:
(x 2 + y 2)2 – 2a 2(x 2 – y 2) = b 4 – a 4.
The general properties of the lemniscate were discovered by Giovanni Fagnano (1715–1797) in 1750; Leonhard Euler's investigations of the length of arc of the curve (1751) led to later work on elliptic functions.
There is a relationship between the lemniscate and the rectangular hyperbola. If a tangent is drawn to the hyperbola and the perpendicular to the tangent is drawn through the origin, the point where the perpendicular meets the tangent is on the lemniscate.


