Cassinian ovals
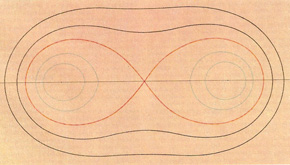
Cassinian ovals: five cases including the lemniscate of Bernoulli (red).
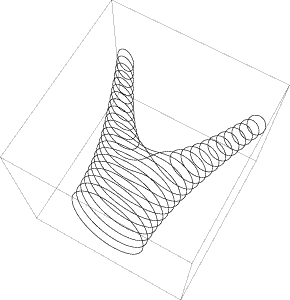
The Cassinian ovals generated as a series of slices.
Cassinian ovals, also known as Cassini's ovals, are a family of curves each member of which is defined as follows: given two points A and B and a constant c2, the locus of points P with PA × PB = c2. The locus has the equation (x2 + y2)2 - 2a2(x2 - y2)2 - a4 + c4 = 0, where a = AB.
Equivalently, Cassinian ovals can be thought of as the set of curves produced when a circular torus is sliced at every possible point parallel to its axis. If c = a, then the curve is a special case known as the lemniscate of Bernoulli (a figure-of-eight type curve).
The ovals are named after the Italian-born astronomer Giovanni Cassini who first investigated then in 1680 while studying the relative motions of the Earth and the Sun. Cassini thought that the Sun traveled round the Earth on one of these curves (rather than the ellipse, as correctly proposed in Kepler's heliocentric scheme), with the Earth at one focus.

