hippopede
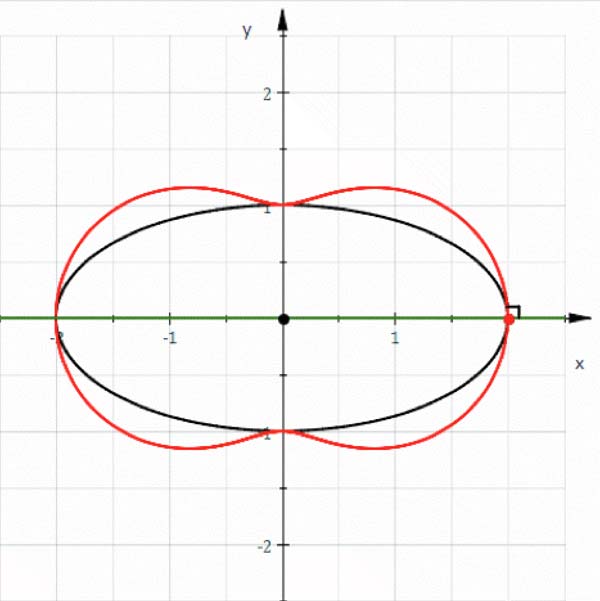
Hippopede (red) given as the pedal curve of an ellipse (black).
The hippopede is a quartic curve described by the equation
(x 2 + y 2) 2 + 4b(b – a)(x 2 + y 2) – 4b 2x 2 = 0
where a and b are positive constants. 'Hippopede' means literally "foot of a horse." It is often known as the hippopede of Proclus, after Proclus who was the first to study it, together with Eudoxus (who used it in his theory of how the planets move), and also the horse fetter and the curve of Booth because of work done on it by J. Booth (1810–1878).
Any hippopede is the intersection of a torus (donut) with one of its tangent planes – that is, a plane parallel to its axis of rotational symmetry. The curve takes any of a variety of forms depending on where the donut is sliced. It may be a simple oval, an indented oval or elliptical lemniscate of Booth (0 < b < a), two isolated circles, or a figure-eight curve or hyperbolic lemniscate of Booth (0 < a < b).


