curve of constant width
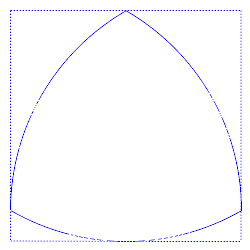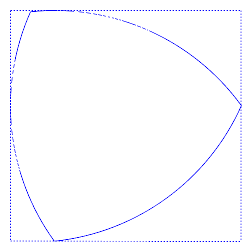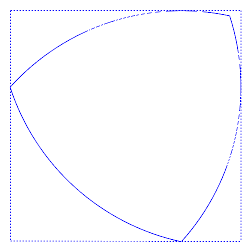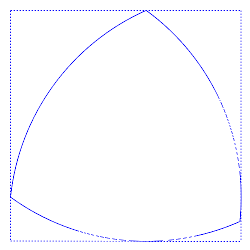
A Reuleaux triangle is a curve of constant width. It can be rotated whilst always touching each side of the square in a single point.
A curve of constant width is a curve that, when rotated in a square, makes continuous contact with all four sides. It may seem, at first sight, as if there is only one such curve – a circle. But, in fact, there are infinitely many different curves of constant width. The circle is the one with the largest area.
The simplest non-circular curve of constant width, and the one with the smallest area, is the Reuleaux triangle. Others can be constructed starting with equilateral (but not necessarily equiangular) stars.
Every curve of constant width is convex. Moreover, Barbier's theorem states that every curve of constant width w has the same perimeter, πw. (The width of a convex figure is defined as the distance between parallel lines – known as supporting lines – that bound it.)
A curve of constant width can be used in a special drill chuck to cut square holes.
A generalization gives solids of constant width. These do not have the same surface area for a given width, but their shadows are curves of constant width.


